【题目】在直角坐标系![]() 中,直线
中,直线![]() ,圆
,圆![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 可得出曲线
可得出曲线![]() 的极坐标方程;
的极坐标方程;
(2)解法一:求出直线![]() 的普通方程,利用点到直线的距离公式计算出圆
的普通方程,利用点到直线的距离公式计算出圆![]() 的圆心到直线
的圆心到直线![]() 的距离
的距离![]() ,再利用勾股定理计算出
,再利用勾股定理计算出![]() ;
;
解法二:设点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,将圆
,将圆![]() 的方程化为极坐标方程,并将直线
的方程化为极坐标方程,并将直线![]() 的方程与圆
的方程与圆![]() 的极坐标方程联立,得出关于
的极坐标方程联立,得出关于![]() 的二次方程,列出韦达定理,可得出
的二次方程,列出韦达定理,可得出![]() ,从而计算出
,从而计算出![]() .
.
(1)由直线![]() ,可得
,可得![]() 的极坐标方程为
的极坐标方程为![]() ;
;
(2)解法一:由直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
得直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() .
.
圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,
,
则圆心到直线的距离![]() ,
,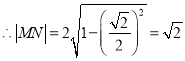 ;
;
解法二:圆![]() 的普通方程为
的普通方程为![]() ,
,
化为极坐标方程得![]() ,
,
设点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,
,
将直线![]() 的极坐标方程代入圆
的极坐标方程代入圆![]() 的极坐标方程得
的极坐标方程得![]() ,
,![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
因此,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对在直角坐标系的第一象限内的任意两点作如下定义:若
 ,那么称点
,那么称点 是点
是点 的“上位点”同时点
的“上位点”同时点 是点
是点 的“下位点”
的“下位点”(1)试写出点
 的一个“上位点”坐标和一个“下位点”坐标;
的一个“上位点”坐标和一个“下位点”坐标;(2)已知点
 是点
是点 的“上位点”,判断是否一定存在点
的“上位点”,判断是否一定存在点 满足既是点
满足既是点 的“上位点”,又是点
的“上位点”,又是点 的“下位点”若存在,写出一个点
的“下位点”若存在,写出一个点 坐标,并证明:若不存在,则说明理由;
坐标,并证明:若不存在,则说明理由;(3)设正整数
 满足以下条件:对集合
满足以下条件:对集合 ,总存在
,总存在 ,使得点
,使得点 既是点
既是点 的“下位点”,又是点
的“下位点”,又是点 的“上位点”,求正整数
的“上位点”,求正整数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:中位数为2,极差为5; 乙地:总体平均数为2,众数为2;
丙地:总体平均数为1,总体方差大于0; 丁地:总体平均数为2,总体方差为3.
A.甲地B.乙地C.丙地D.丁地
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人经营一个抽奖游戏,顾客花费
 元钱可购买一次游戏机会,每次游戏中,顾客从装有
元钱可购买一次游戏机会,每次游戏中,顾客从装有 个黑球,
个黑球, 个红球,
个红球, 个白球的不透明袋子中依次不放回地摸出
个白球的不透明袋子中依次不放回地摸出 个球(除颜色外其他都相同),根据摸出的球的颜色情况进行兑奖.顾客获得一等奖、二等奖、三等奖、四等奖时分别可领取奖金
个球(除颜色外其他都相同),根据摸出的球的颜色情况进行兑奖.顾客获得一等奖、二等奖、三等奖、四等奖时分别可领取奖金 元,
元, 元、
元、 元、
元、 元.若经营者将顾客摸出的
元.若经营者将顾客摸出的 个球的颜色情况分成以下类别:
个球的颜色情况分成以下类别: :
: 个黑球,
个黑球, 个红球;
个红球; :
: 个红球;
个红球; :恰有
:恰有 个白球;
个白球; :恰有
:恰有 个白球;
个白球; :
: 个白球,且经营者计划将五种类别按照发生机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖五个层次.
个白球,且经营者计划将五种类别按照发生机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖五个层次.(1)请写出一至四等奖分别对应的类别(写出字母即可);
(2)若经营者不打算在这个游戏的经营中亏本,求
 的最大值;
的最大值;(3)若
 ,当顾客摸出的第一个球是红球时,求他领取的奖金的平均值.
,当顾客摸出的第一个球是红球时,求他领取的奖金的平均值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机生产厂商为迎接5G时代的到来,要生产一款5G手机,在生产之前,该公司对手机屏幕的需求尺寸进行社会调查,共调查了400人,将这400人按对手机屏幕的需求尺寸分为6组,分别是:
 ,
, ,
, ,
, ,
, ,
, (单位:英寸),得到如下频率分布直方图:
(单位:英寸),得到如下频率分布直方图:
其中,屏幕需求尺寸在
 的一组人数为50人.
的一组人数为50人.(1)求a和b的值;
(2)用分层抽样的方法在屏幕需求尺寸为
 和
和 两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?(3)若以厂家此次调查结果的频率作为概率,市场随机调查两人,这两人屏幕需求尺寸分别在
 和
和 的概率是多少?
的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,函数
,函数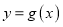 为函数
为函数 的反函数.
的反函数.(1)求函数
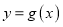 的解析式;
的解析式;(2)若方程
 恰有一个实根,求实数
恰有一个实根,求实数 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意 ,当
,当 时,满足
时,满足 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(2017·长春市二模)如图,在四棱锥
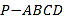 中,底面
中,底面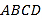 是菱形,
是菱形,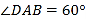 ,
,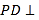 平面
平面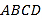 ,
,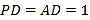 ,点
,点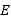 ,
,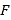 分别为
分别为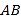 和
和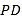 中点.
中点.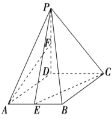
(1)求证:直线
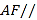 平面
平面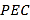 ;
;(2)求
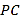 与平面
与平面 所成角的正弦值.
所成角的正弦值.
相关试题

