【题目】已知函数![]() ,函数
,函数![]() 为函数
为函数![]() 的反函数.
的反函数.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 恰有一个实根,求实数
恰有一个实根,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,当
,当![]() 时,满足
时,满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)令![]() 求解即可.
求解即可.
(2)化简等式得![]() ,再分情况讨论即可.
,再分情况讨论即可.
(3)根据![]() 分析
分析![]() 的单调性与最值,利用二次函数的取值范围求解即可.
的单调性与最值,利用二次函数的取值范围求解即可.
解:(1)因为![]() 为函数
为函数![]() 的反函数,
的反函数,
故![]() ,
,
得![]() ,
,
所以![]() ;
;
(2)由![]() 得
得![]() ;
;
当![]() 时,
时,![]() ,经检验,满足题意;
,经检验,满足题意;
当![]() 时,
时,![]() ,经检验,满足题意;
,经检验,满足题意;
当![]() 且
且![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
若![]() 是原方程的解,当且仅当
是原方程的解,当且仅当![]() ,即
,即![]() ,
,
若![]() 是原方程的解,当且仅当
是原方程的解,当且仅当![]() ,即
,即![]() ,
,
于是满足题意的![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.
(3)不妨令![]() ,则
,则![]() ,
,
即函数![]() 在
在![]() 上为减函数;
上为减函数;
![]() ,
,![]() ,
,
因为当![]() ,满足
,满足![]() ,
,
故只需![]() ,
,
即![]() 对任意
对任意![]() 成立.
成立.
因为![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人经营一个抽奖游戏,顾客花费
 元钱可购买一次游戏机会,每次游戏中,顾客从装有
元钱可购买一次游戏机会,每次游戏中,顾客从装有 个黑球,
个黑球, 个红球,
个红球, 个白球的不透明袋子中依次不放回地摸出
个白球的不透明袋子中依次不放回地摸出 个球(除颜色外其他都相同),根据摸出的球的颜色情况进行兑奖.顾客获得一等奖、二等奖、三等奖、四等奖时分别可领取奖金
个球(除颜色外其他都相同),根据摸出的球的颜色情况进行兑奖.顾客获得一等奖、二等奖、三等奖、四等奖时分别可领取奖金 元,
元, 元、
元、 元、
元、 元.若经营者将顾客摸出的
元.若经营者将顾客摸出的 个球的颜色情况分成以下类别:
个球的颜色情况分成以下类别: :
: 个黑球,
个黑球, 个红球;
个红球; :
: 个红球;
个红球; :恰有
:恰有 个白球;
个白球; :恰有
:恰有 个白球;
个白球; :
: 个白球,且经营者计划将五种类别按照发生机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖五个层次.
个白球,且经营者计划将五种类别按照发生机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖五个层次.(1)请写出一至四等奖分别对应的类别(写出字母即可);
(2)若经营者不打算在这个游戏的经营中亏本,求
 的最大值;
的最大值;(3)若
 ,当顾客摸出的第一个球是红球时,求他领取的奖金的平均值.
,当顾客摸出的第一个球是红球时,求他领取的奖金的平均值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
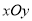 中,直线
中,直线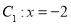 ,圆
,圆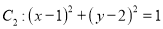 .以原点
.以原点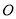 为极点,
为极点,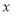 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求
 的极坐标方程;
的极坐标方程;(2)若直线
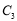 的极坐标方程为
的极坐标方程为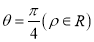 ,设
,设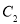 与
与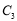 的交点为
的交点为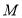 、
、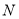 ,求
,求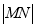 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机生产厂商为迎接5G时代的到来,要生产一款5G手机,在生产之前,该公司对手机屏幕的需求尺寸进行社会调查,共调查了400人,将这400人按对手机屏幕的需求尺寸分为6组,分别是:
 ,
, ,
, ,
, ,
, ,
, (单位:英寸),得到如下频率分布直方图:
(单位:英寸),得到如下频率分布直方图:
其中,屏幕需求尺寸在
 的一组人数为50人.
的一组人数为50人.(1)求a和b的值;
(2)用分层抽样的方法在屏幕需求尺寸为
 和
和 两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?(3)若以厂家此次调查结果的频率作为概率,市场随机调查两人,这两人屏幕需求尺寸分别在
 和
和 的概率是多少?
的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(2017·长春市二模)如图,在四棱锥
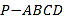 中,底面
中,底面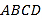 是菱形,
是菱形,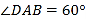 ,
,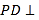 平面
平面 ,
,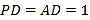 ,点
,点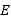 ,
,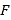 分别为
分别为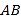 和
和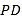 中点.
中点.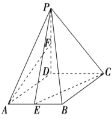
(1)求证:直线
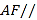 平面
平面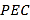 ;
;(2)求
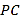 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
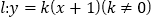 与椭圆
与椭圆 相交于
相交于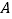 ,
,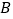 两个不同的点,与
两个不同的点,与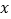 轴相交于点
轴相交于点 ,
,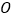 为坐标原点.
为坐标原点.(1)证明:
 ;
;(2)若
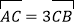 ,求
,求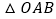 的面积取得最大值时椭圆的方程.
的面积取得最大值时椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
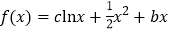
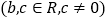 ,且
,且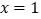 为
为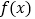 的极值点.
的极值点.(Ⅰ) 若
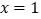 为
为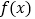 的极大值点,求
的极大值点,求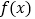 的单调区间(用
的单调区间(用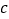 表示);
表示);(Ⅱ)若
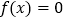 恰有1解,求实数
恰有1解,求实数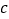 的取值范围.
的取值范围.
相关试题

