【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)求在抽取的40名学生中月上网次数不少于15次的学生人数;
(Ⅲ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取2人 ,求至少抽到1名女生
的概率.

参考答案:
【答案】(I)![]() ;(II)
;(II)![]() ;(III)
;(III)![]() .
.
【解析】
试题分析:(I)利用频率分布直方图小长方形面积等于![]() ,列式计算得
,列式计算得![]() ;(II)女生的频率为
;(II)女生的频率为![]() ,抽取
,抽取![]() 人,男生频率也是
人,男生频率也是![]() ,抽取
,抽取![]() 人,共
人,共![]() 人;(III)上网超过
人;(III)上网超过![]() 次的男生有
次的男生有![]() 人,女生有
人,女生有![]() 人,用列举法列举出可能性一共有
人,用列举法列举出可能性一共有![]() 种,其中符合题意要求的有
种,其中符合题意要求的有![]() 种,故概率为
种,故概率为![]() .
.
试题解析:(Ⅰ)![]() .
.
(Ⅱ)在所抽取的女生中,月上网次数不少于![]() 次的学生频率为
次的学生频率为![]() ,所以,在所抽取的女生中,月上网次数不少于
,所以,在所抽取的女生中,月上网次数不少于![]() 次的学生有
次的学生有![]() 人.
人.
在所抽取的男生中,月上网次数不少于![]() 次的学生频率为
次的学生频率为![]() ,所以,在所抽取的男生中,月上网次数不少于
,所以,在所抽取的男生中,月上网次数不少于![]() 次的学生有
次的学生有![]() 人.
人.
故抽取的![]() 名学生中月上网次数不少于
名学生中月上网次数不少于![]() 次的学生人数有
次的学生人数有![]() 人.
人.
(Ⅲ)记“在抽取的![]() 名学生中,从月上网次数不少于
名学生中,从月上网次数不少于![]() 次的学生中随机抽取
次的学生中随机抽取![]() 人,至少抽到
人,至少抽到![]() 名女生”为事件
名女生”为事件![]() ,
,
在抽取的女生中,月上网次数不少于![]() 次的学生频率为
次的学生频率为![]() ,人数为
,人数为![]() 人,在抽取的男生中,月上网次数不少于
人,在抽取的男生中,月上网次数不少于![]() 次的学生频率为
次的学生频率为![]() ,人数为
,人数为![]() 人,
人,
记这![]() 名女生为
名女生为![]() ,
,![]() ,这
,这![]() 名男生为
名男生为![]() ,
,![]() ,
,![]() ,
,
则在抽取的![]() 名学生中,从月上网次数不少于
名学生中,从月上网次数不少于![]() 次的学生中随机抽取
次的学生中随机抽取![]() 人,所有可能结果有
人,所有可能结果有![]() 种,即
种,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而事件![]() 包含的结果有
包含的结果有![]() 种,它们是
种,它们是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由与圆心距离相等的两条弦长相等,想到与球心距离相等的两个截面圆的面积相等,用的是( )
A. 三段论推理 B. 类比推理 C. 归纳推理 D. 传递性关系推理
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
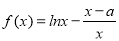 ,其中
,其中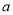 为常数.
为常数.(1)若曲数
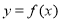 在点
在点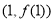 处的切线与直线
处的切线与直线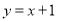 垂直,求函数
垂直,求函数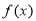 的单调递减区间;
的单调递减区间;(2)若函数
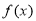 在区间[1,3]上的最小值为
在区间[1,3]上的最小值为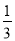 ,求
,求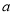 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)是否存在实数
 ,使
,使 恒成立,若存在,求出实数
恒成立,若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
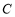 的极坐标方程为
的极坐标方程为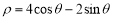 ,直线
,直线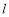 的参数方程为
的参数方程为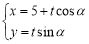 (
(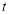 为参数).若直线
为参数).若直线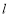 与圆
与圆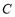 相交于不同的两点
相交于不同的两点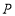 ,
,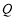 .
.(Ⅰ)写出圆
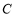 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;(Ⅱ)若弦长
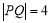 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
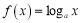 ,
,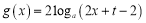 ,其中
,其中 且
且 ,
,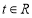 .
.(1)若
 ,且
,且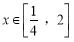 时,
时,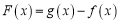 的最小值是
的最小值是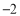 ,求实数
,求实数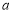 的值;
的值;(2)若
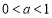 ,且
,且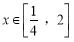 时,有
时,有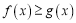 恒成立,求实数
恒成立,求实数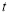 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
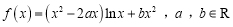 .
.(Ⅰ)当
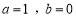 时,求曲线
时,求曲线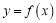 在点
在点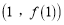 处的切线方程;
处的切线方程;(Ⅱ)当
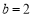 时,若对任意
时,若对任意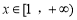 ,不等式
,不等式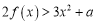 恒成立,求实数
恒成立,求实数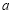 的取值范围.
的取值范围.
相关试题

