【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,
两点,![]() 是直线
是直线![]() 上的点,且
上的点,且![]() ,当
,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(Ⅰ)![]() ,曲线
,曲线![]() :
:![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:
(Ⅰ)将直线的参数方程消去参数可得普通方程,利用转化公式可将曲线C的极坐标方程化为直角坐标方程.(Ⅱ)根据直线的参数方程中参数t的几何意义求解,并结合三角函数的知识可得当![]() 时,
时,![]() 最大,此时
最大,此时![]() 最大.然后利用参数方程可得点
最大.然后利用参数方程可得点![]() 的坐标.
的坐标.
试题解析:
(Ⅰ)由![]() (
(![]() 为参数)消去参数可得
为参数)消去参数可得![]() ,
,
∴直线![]() 的普通方程为
的普通方程为![]() .
.
由![]() 可得
可得![]() ,
,
将![]() 代入上式可得
代入上式可得![]() ,
,
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅱ)设直线![]() 上的三点
上的三点![]() 所对应的参数分别为
所对应的参数分别为![]() ,
,
将![]() 代入
代入![]() ,
,
整理得![]() ,
,
则![]() ,
,
![]() 与
与![]() 异号,
异号,
由![]() ,得
,得![]() ,
,
![]()
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 最大,此时
最大,此时![]() 最大,
最大,
且![]() ,此时
,此时![]() ,代入
,代入![]() 可得此时点
可得此时点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公交车的数量太多容易造成资源浪费,太少又难以满足乘客的需求,为了合理布置车辆,公交公司在2路车的乘客中随机调查了50名乘客,经整理,他们候车时间(单位:
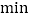 )的茎叶图如下:
)的茎叶图如下:
(Ⅰ)将候车时间分为
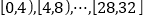 八组,作出相应的频率分布直方图;
八组,作出相应的频率分布直方图;
(Ⅱ)若公交公司将2路车发车时间调整为每隔15
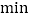 发一趟车,那么上述样本点将发生变化(例如候车时间为9
发一趟车,那么上述样本点将发生变化(例如候车时间为9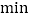 的不变,候车时间为17
的不变,候车时间为17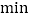 的变为2
的变为2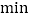 ),现从2路车的乘客中任取5人,设其中候车时间不超过10
),现从2路车的乘客中任取5人,设其中候车时间不超过10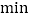 的乘客人数为
的乘客人数为 ,求
,求 的数学期望.
的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
 万件,需另投入成本为
万件,需另投入成本为 ,当年产量不足80万件时,
,当年产量不足80万件时, (万元).当年产量不小于80万件时,
(万元).当年产量不小于80万件时, (万元).每件商品售价为50元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为50元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润
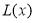 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;(2)年产量为多少万件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)求函数
 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 的单调区间;
的单调区间;(3) 求证:当
 时,
时, 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,(1)若不等式
 的解集为
的解集为 ,求
,求 的值;
的值;(2)若
 ,求
,求 的最小值.
的最小值.(3)若
 求不等式
求不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加
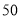 元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费
元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费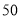 元.
元.(1)当每辆车的月租金定为
 元时,能租出多少辆车?
元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
① 函数
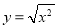 与函数
与函数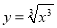 表示同一个函数.
表示同一个函数.② 奇函数的图象一定过直角坐标系的坐标原点.
③ 函数
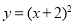 的图象可由
的图象可由 的图象向左平移
的图象向左平移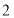 个单位长度得到.
个单位长度得到.④ 若函数
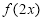 的定义域为
的定义域为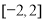 ,则函数
,则函数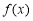 的定义域为
的定义域为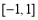 .
.其中正确命题的序号是_________ (填上所有正确命题的序号) .
相关试题

