【题目】设函数![]() ,
,
(1)若不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值.
的最小值.
(3)若![]() 求不等式
求不等式![]() 的解集.
的解集.
参考答案:
【答案】(1)2;(2)![]() ;(3)分类讨论,详见解析.
;(3)分类讨论,详见解析.
【解析】
(1)根据不等式与相应的方程之间的关系得出关于![]() 的方程组,求解可得出
的方程组,求解可得出![]() 的值;
的值;
(2)由![]() 得
得![]() ,再代入
,再代入![]() 中运用均值不等式可求得最小值;
中运用均值不等式可求得最小值;
(3)由已知将不等式![]() 化为
化为![]() ,即
,即![]() ,对
,对![]() 分①
分①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 四种情况分别讨论得出不等式的解集.
四种情况分别讨论得出不等式的解集.
(1)由不等式![]() 的解集为
的解集为![]() 可得:方程
可得:方程![]() 的两根为
的两根为![]() ,3且
,3且![]() ,
,
由根与系数的关系可得:![]() ,
,
所以![]()
(2)由已知得![]() ,则
,则
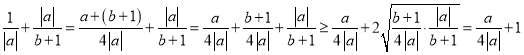 ,
,
当![]() 时,
时,![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立);
时等号成立);
当![]() 时,
时,![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立);
时等号成立);
所以![]() 的最小值为
的最小值为![]() ;
;
(3)由![]() 得
得![]() ,
,
又因为![]() 所以不等式
所以不等式![]() 化为
化为![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,原不等式
,原不等式![]() 或
或![]()
若![]() ,原不等式
,原不等式![]() 此时原不等式的解的情况应由
此时原不等式的解的情况应由![]() 与1的大小关系决定,故
与1的大小关系决定,故
(1)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ;
;
(2)当![]() 时,
时,![]() ,不等式
,不等式![]()
![]() ;
;
(3)当![]() 时,
时,![]() ,不等式
,不等式![]()
![]() .
.
综上所述,不等式的解集为:
①当![]() 时,
时,![]() 或
或![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() ;
;
④当![]() 时,
时,![]() .
.
故得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
 万件,需另投入成本为
万件,需另投入成本为 ,当年产量不足80万件时,
,当年产量不足80万件时, (万元).当年产量不小于80万件时,
(万元).当年产量不小于80万件时, (万元).每件商品售价为50元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为50元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润
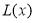 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;(2)年产量为多少万件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)求函数
 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 的单调区间;
的单调区间;(3) 求证:当
 时,
时, 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数,
为参数,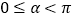 ),以
),以 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求直线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(Ⅱ)设
 ,直线
,直线 交曲线
交曲线 于
于 两点,
两点, 是直线
是直线 上的点,且
上的点,且 ,当
,当 最大时,求点
最大时,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加
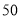 元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费
元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费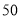 元.
元.(1)当每辆车的月租金定为
 元时,能租出多少辆车?
元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
① 函数
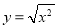 与函数
与函数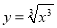 表示同一个函数.
表示同一个函数.② 奇函数的图象一定过直角坐标系的坐标原点.
③ 函数
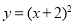 的图象可由
的图象可由 的图象向左平移
的图象向左平移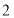 个单位长度得到.
个单位长度得到.④ 若函数
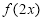 的定义域为
的定义域为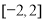 ,则函数
,则函数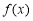 的定义域为
的定义域为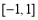 .
.其中正确命题的序号是_________ (填上所有正确命题的序号) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—5:不等式选讲
已知函数
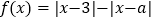 .
.(1)当
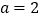 时,解不等式
时,解不等式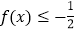 ;
;(2)若存在实数
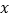 ,使得不等式
,使得不等式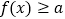 成立,求实
成立,求实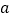 的取值范围.
的取值范围.
相关试题

