【题目】已知向量![]() ,
,![]() ,存在非零实数
,存在非零实数![]() 和
和![]() ,使得向量
,使得向量![]() ,
,![]() ,且
,且![]() .问
.问![]() 是否存在最小值?若存在,求其最小值;若不存在,说明理由.
是否存在最小值?若存在,求其最小值;若不存在,说明理由.
参考答案:
【答案】存在最小值,最小值![]() .
.
【解析】试题分析:根据向量数量积的坐标公式和性质,分别求出|![]() |=2,|
|=2,|![]() |=1且
|=1且![]()
![]() =0,由此将
=0,由此将![]()
![]() =0化简整理得到k=
=0化简整理得到k=![]() (t3﹣3t).将此代入
(t3﹣3t).将此代入![]() ,可得关于t的二次函数,根据二次函数的单调性即可得到
,可得关于t的二次函数,根据二次函数的单调性即可得到![]() 的最小值.
的最小值.
试题解析:由已知得, ![]() ,
,![]() ,
,![]() .由
.由![]() 得,
得, ![]() ,
,
即![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
点晴:平面向量的数量积计算问题,往往有两种形式,一是利用数量积的定义式,二是利用数量积的坐标运算公式,涉及几何图形的问题,先建立适当的平面直角坐标系,可起到化繁为简的妙用. 利用向量夹角公式、模公式及向量垂直的充要条件,可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决.列出方程组求得![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司一年经销某种商品,年销售量400吨,每吨进价5万元,每吨销售价8万元.全年进货若干次,每次都购买x吨,运费为每次2万元,一年的总存储费用为2x万元.
(1)求该公司经销这种商品一年的总利润y与x的函数关系;
(2)要使一年的总利润最大,则每次购买量为多少?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)已知a,b为正整数,a≠b,x>0,y>0.试比较 +
+ 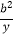 与
与 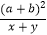 的大小,并指出两式相等的条件.
的大小,并指出两式相等的条件.
(2)用(1)所得结论,求函数y= +
+ 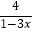 ,x∈(0,
,x∈(0,  )的最小值.
)的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥S﹣ABC中,AB⊥BC,AB=BC=
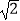 , SA=SC=2,二面角S﹣AC﹣B的余弦值是
, SA=SC=2,二面角S﹣AC﹣B的余弦值是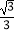 , 若S、A、B、C都在同一球面上,则该球的表面积是
, 若S、A、B、C都在同一球面上,则该球的表面积是 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
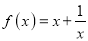 的图象为
的图象为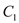 ,
, 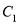 关于点
关于点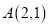 对称的图象为
对称的图象为 ,
, 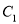 对应的函数为
对应的函数为 .
.(Ⅰ)求
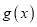 的解析式;
的解析式;(Ⅱ)若直线
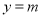 与
与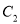 只有一个交点,求
只有一个交点,求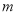 的值和交点坐标.
的值和交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(2,5)和(8,3)是函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象仅有的两个交点,那么a+b+c+d的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是R上的奇函数,且
是R上的奇函数,且 的图象关于
的图象关于 对称,当
对称,当 时,
时,  ,
,(Ⅰ)当
 时,求
时,求 的解析式;
的解析式;(Ⅱ)计算
 的值.
的值.
相关试题

