【题目】对于数集X={﹣1,x1 , x2 , …,xn},其中0<x1<x2<…<xn , n≥2,定义向量集Y={ ![]() =(s,t),s∈X,t∈X},若对任意
=(s,t),s∈X,t∈X},若对任意 ![]() ,存在
,存在 ![]() ,使得
,使得 ![]() ,则称X具有性质P.例如{﹣1,1,2}具有性质P.
,则称X具有性质P.例如{﹣1,1,2}具有性质P.
(1)若x>2,且{﹣1,1,2,x}具有性质P,求x的值;
(2)若X具有性质P,求证:1∈X,且当xn>1时,x1=1;
(3)若X具有性质P,且x1=1、x2=q(q为常数),求有穷数列x1 , x2 , …,xn的通项公式.
参考答案:
【答案】
(1)解:选取 ![]() =(x,2),则Y中与
=(x,2),则Y中与 ![]() 垂直的元素必有形式(﹣1,b),所以x=2b,
垂直的元素必有形式(﹣1,b),所以x=2b,
又∵x>2,∴只有b=2,从而x=4.
(2)解:取 ![]() =(x1,x1)∈Y,设
=(x1,x1)∈Y,设 ![]() =(s,t)∈Y,满足
=(s,t)∈Y,满足 ![]() ,可得(s+t)x1=0,s+t=0,所以s、t异号.
,可得(s+t)x1=0,s+t=0,所以s、t异号.
因为﹣1是数集X中唯一的负数,所以s、t中的负数必为﹣1,另一个数是1,所以1∈X,
假设xk=1,其中1<k<n,则0<x1<1<xn.
再取 ![]() =(x1,xn)∈Y,设
=(x1,xn)∈Y,设 ![]() =(s,t)∈Y,满足
=(s,t)∈Y,满足 ![]() ,可得sx1+txn=0,
,可得sx1+txn=0,
所以s、t异号,其中一个为﹣1
①若s=﹣1,则x1=txn>t≥x1,矛盾;
②若t=﹣1,则xn=sx1<s≤xn,矛盾;
说明假设不成立,由此可得当xn>1时,x1=1.
(3)解:[解法一]猜想:xi=qi﹣1,i=1,2,3,…,n
记Ak═{﹣1,x1,x2,…,xk},k=2,3,…,n
先证明若Ak+1具有性质P,则Ak也具有性质P.
任取 ![]() =(s,t),s、t∈Ak,当s、t中出现﹣1时,显然有
=(s,t),s、t∈Ak,当s、t中出现﹣1时,显然有 ![]() 满足
满足 ![]()
当s、t中都不是﹣1时,满足s≥1且t≥1.
因为Ak+1具有性质P,所以有 ![]() =(s1,t1),s1、t1∈Ak+1,使得
=(s1,t1),s1、t1∈Ak+1,使得 ![]() ,从而s1、t1其中有一个为﹣1
,从而s1、t1其中有一个为﹣1
不妨设s1=﹣1,
假设t1∈Ak+1,且t1Ak,则t1=xk+1.由(s,t)(﹣1,xk+1)=0,得s=txk+1≥xk+1,与s∈Ak矛盾.
所以t1∈Ak,从而Ak也具有性质P.
再用数学归纳法,证明xi=qi﹣1,i=1,2,3,…,n
当n=2时,结论显然成立;
假设当n=k时,Ak═{﹣1,x1,x2,…,xk}具有性质P,则xi=qi﹣1,i=1,2,…,k
当n=k+1时,若Ak+1═{﹣1,x1,x2,…,xk+1}具有性质P,则Ak═{﹣1,x1,x2,…,xk}具有性质P,
所以Ak+1═{﹣1,q,q2,…,qk﹣1,xk+1}.
取 ![]() =(xk+1,q),并设
=(xk+1,q),并设 ![]() =(s,t)∈Y,满足
=(s,t)∈Y,满足 ![]() ,由此可得s=﹣1或t=﹣1
,由此可得s=﹣1或t=﹣1
若t=﹣1,则xk+1= ![]() ,不可能
,不可能
所以s=﹣1,xk+1=qt=qj≤qk且xk+1>qk﹣1,因此xk+1=qk综上所述,xi=qi﹣1,i=1,2,3,…,n
[解法二]设 ![]() =(s1,t1),
=(s1,t1), ![]() =(s2,t2),则
=(s2,t2),则 ![]() 等价于
等价于 ![]()
记B={ ![]() |s∈X,t∈X且|s|>|t|},则数集X具有性质P,当且仅当数集B关于原点对称
|s∈X,t∈X且|s|>|t|},则数集X具有性质P,当且仅当数集B关于原点对称
注意到﹣1是集合X中唯一的负数,B∩(﹣∞,0)={﹣x2,﹣x3,﹣x4,…,﹣xn},共有n﹣1个数.
所以B∩(0,+∞)也有n﹣1个数.
由于 ![]() <
< ![]() <
< ![]() <…<
<…< ![]() ,已经有n﹣1个数
,已经有n﹣1个数
对以下三角形数阵: ![]() <
< ![]() <
< ![]() <…<
<…< ![]() ,
,
![]() <
< ![]() <
< ![]() <…<
<…< ![]()
![]()
注意到 ![]() >
> ![]() >
> ![]() >…>
>…> ![]() ,所以
,所以 ![]() =
= ![]() =…=
=…= ![]()
从而数列的通项公式是xk=x1( ![]() )k﹣1=qk﹣1,k=1,2,3,…,n.
)k﹣1=qk﹣1,k=1,2,3,…,n.
【解析】(1)在Y中取 ![]() =(x,2),根据数量积的坐标公式,可得Y中与
=(x,2),根据数量积的坐标公式,可得Y中与 ![]() 垂直的元素必有形式(﹣1,b),所以x=2b,结合x>2,可得x的值.(2)取
垂直的元素必有形式(﹣1,b),所以x=2b,结合x>2,可得x的值.(2)取 ![]() =(x1 , x1),
=(x1 , x1), ![]() =(s,t)根据
=(s,t)根据 ![]() ,化简可得s+t=0,所以s、t异号.而﹣1是数集X中唯一的负数,所以s、t中的负数必为﹣1,另一个数是1,从而证出1∈X,最后通过反证法,可以证明出当xn>1时,x1=1.(3)[解法一]先猜想结论:xi=qi﹣1 , i=1,2,3,…,n.记Ak═{﹣1,x1 , x2 , …,xk},k=2,3,…,n,通过反证法证明出引理:若Ak+1具有性质P,则Ak也具有性质P.最后用数学归纳法,可证明出xi=qi﹣1 , i=1,2,3,…,n;
,化简可得s+t=0,所以s、t异号.而﹣1是数集X中唯一的负数,所以s、t中的负数必为﹣1,另一个数是1,从而证出1∈X,最后通过反证法,可以证明出当xn>1时,x1=1.(3)[解法一]先猜想结论:xi=qi﹣1 , i=1,2,3,…,n.记Ak═{﹣1,x1 , x2 , …,xk},k=2,3,…,n,通过反证法证明出引理:若Ak+1具有性质P,则Ak也具有性质P.最后用数学归纳法,可证明出xi=qi﹣1 , i=1,2,3,…,n;
[解法二]设 ![]() =(s1 , t1),
=(s1 , t1), ![]() =(s2 , t2),则
=(s2 , t2),则 ![]() 等价于
等价于 ![]() ,得到一正一负的特征,再记B={
,得到一正一负的特征,再记B={ ![]() |s∈X,t∈X且|s|>|t|},则可得结论:数集X具有性质P,当且仅当数集B关于原点对称.又注意到﹣1是集合X中唯一的负数,B∩(﹣∞,0)={﹣x2 , ﹣x3 , ﹣x4 , …,﹣xn},共有n﹣1个数,所以B∩(0.+∞)也有n﹣1个数.最后结合不等式的性质,结合三角形数阵加以说明,可得
|s∈X,t∈X且|s|>|t|},则可得结论:数集X具有性质P,当且仅当数集B关于原点对称.又注意到﹣1是集合X中唯一的负数,B∩(﹣∞,0)={﹣x2 , ﹣x3 , ﹣x4 , …,﹣xn},共有n﹣1个数,所以B∩(0.+∞)也有n﹣1个数.最后结合不等式的性质,结合三角形数阵加以说明,可得 ![]() =
= ![]() =…=
=…= ![]() ,最终得到数列的通项公式是xk=x1(
,最终得到数列的通项公式是xk=x1( ![]() )k﹣1=qk﹣1 , k=1,2,3,…,n.
)k﹣1=qk﹣1 , k=1,2,3,…,n.
【考点精析】利用元素与集合关系的判断对题目进行判断即可得到答案,需要熟知对象![]() 与集合
与集合![]() 的关系是
的关系是![]() ,或者
,或者![]() ,两者必居其一.
,两者必居其一.
-
科目: 来源: 题型:
查看答案和解析>>【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,如图是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成
 列联表,并据此资料你是否有
列联表,并据此资料你是否有 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?
注:
 ,其中
,其中 .
.
(2)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(3)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中有2名选手的等级为优秀的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“节约用水”自古以来就是中华民族的优良传统.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如下图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.

(l)求在未来连续3个月里,有连续2个月的月用水量都不低于12吨且另1个月的月用水量低于4吨的概率;
(2)用
 表示在未来3个月里月用水量不低于12吨的月数,求随杌变量
表示在未来3个月里月用水量不低于12吨的月数,求随杌变量 的分布列及数学期望
的分布列及数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知双曲线C1:2x2﹣y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ;
(3)设椭圆C2:4x2+y2=1,若M、N分别是C1、C2上的动点,且OM⊥ON,求证:O到直线MN的距离是定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________. -
科目: 来源: 题型:
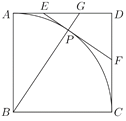
查看答案和解析>>【题目】如图,在边长为6的正方形
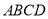 中,弧
中,弧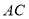 的圆心为
的圆心为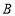 ,过弧
,过弧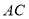 上的点
上的点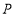 作弧
作弧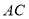 的切线,与
的切线,与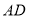 、
、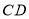 分别相交于点
分别相交于点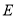 、
、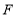 ,
,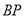 的延长线交
的延长线交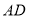 边于点
边于点 .
.
(1)设
 ,
,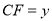 ,求
,求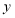 与
与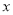 之间的函数解析式,并写出函数定义域;
之间的函数解析式,并写出函数定义域;(2)当
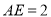 时,求
时,求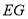 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全一直是人们关心和重视的问题,学校的食品安全更是社会关注的焦点.某中学为了加强食品安全教育,随机询问了36名不同性别的中学生在购买食品时是否看保质期,得到如下“性别”与“是否看保质期”的列联表:
男
女
总计
看保质期
8
22
不看保持期
4
14
总计
(1)请将列联表填写完整,并根据所填的列联表判断,能否有
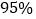 的把握认为“性别”与“是否看保质期”有关?
的把握认为“性别”与“是否看保质期”有关?(2)从被询问的14名不看保质期的中学生中,随机抽取3名,求抽到女生人数
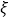 的分布列和数学期望.
的分布列和数学期望.附:
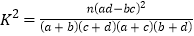 ,(
,(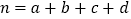 ).
).临界值表:

0.15
0.10
0.05
0.025
0.010
0.005
0.001
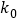
2.072
2.706
3.841
5.024
6.635
7.879
10.828
相关试题

