【题目】如图,在边长为6的正方形![]() 中,弧
中,弧![]() 的圆心为
的圆心为![]() ,过弧
,过弧![]() 上的点
上的点![]() 作弧
作弧![]() 的切线,与
的切线,与![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() ,
,![]() 的延长线交
的延长线交![]() 边于点
边于点![]() .
.
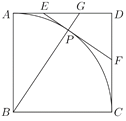
(1)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出函数定义域;
之间的函数解析式,并写出函数定义域;
(2)当![]() 时,求
时,求![]() 的长.
的长.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据切线长定理求得![]() 的长,在直角三角形
的长,在直角三角形![]() 中利用勾股定理求得
中利用勾股定理求得![]() 与
与![]() 的关系式.(2)以
的关系式.(2)以![]() 为平面直角坐标系原点
为平面直角坐标系原点![]() 分别为
分别为![]() 轴建立平面直角坐标系,又
轴建立平面直角坐标系,又![]() 坐标,求得直线
坐标,求得直线![]() 的斜率,进而求得直线
的斜率,进而求得直线![]() 的斜率,由此求得
的斜率,由此求得![]() 长,进而求得
长,进而求得![]() 的长.
的长.
(1)根据切线长定理得![]() ,且
,且![]() ,直角三角形
,直角三角形![]() 中由勾股定理得
中由勾股定理得![]() ,化简得
,化简得![]() ,由
,由![]() ,解得
,解得![]() ,也即函数定义域为
,也即函数定义域为![]() .所以函数解析式为
.所以函数解析式为![]() .(2)当
.(2)当![]() 时,由(1)知
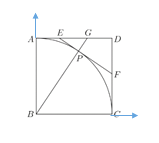
时,由(1)知![]() .以
.以![]() 为平面直角坐标系原点
为平面直角坐标系原点![]() 分别为
分别为![]() 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,所以与
,所以与![]() 垂直的直线
垂直的直线![]() 的斜率为
的斜率为![]() ,而
,而![]() ,所以
,所以![]() ,所以
,所以![]() .即
.即![]() 长为
长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知双曲线C1:2x2﹣y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ;
(3)设椭圆C2:4x2+y2=1,若M、N分别是C1、C2上的动点,且OM⊥ON,求证:O到直线MN的距离是定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集X={﹣1,x1 , x2 , …,xn},其中0<x1<x2<…<xn , n≥2,定义向量集Y={
 =(s,t),s∈X,t∈X},若对任意
=(s,t),s∈X,t∈X},若对任意 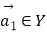 ,存在
,存在  ,使得
,使得  ,则称X具有性质P.例如{﹣1,1,2}具有性质P.
,则称X具有性质P.例如{﹣1,1,2}具有性质P.
(1)若x>2,且{﹣1,1,2,x}具有性质P,求x的值;
(2)若X具有性质P,求证:1∈X,且当xn>1时,x1=1;
(3)若X具有性质P,且x1=1、x2=q(q为常数),求有穷数列x1 , x2 , …,xn的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全一直是人们关心和重视的问题,学校的食品安全更是社会关注的焦点.某中学为了加强食品安全教育,随机询问了36名不同性别的中学生在购买食品时是否看保质期,得到如下“性别”与“是否看保质期”的列联表:
男
女
总计
看保质期
8
22
不看保持期
4
14
总计
(1)请将列联表填写完整,并根据所填的列联表判断,能否有
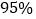 的把握认为“性别”与“是否看保质期”有关?
的把握认为“性别”与“是否看保质期”有关?(2)从被询问的14名不看保质期的中学生中,随机抽取3名,求抽到女生人数
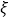 的分布列和数学期望.
的分布列和数学期望.附:
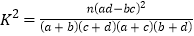 ,(
,(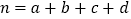 ).
).临界值表:

0.15
0.10
0.05
0.025
0.010
0.005
0.001
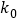
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
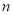 为正整数,集合
为正整数,集合 (
(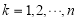 ),对于集合
),对于集合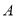 中的任意元素
中的任意元素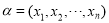 和
和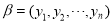 ,记
,记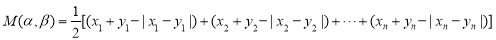 .
.(1)当
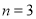 时,若
时,若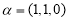 ,
,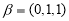 ,求
,求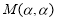 和
和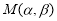 的值;
的值;(2)当
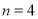 时,设
时,设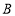 是
是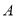 的子集,且满足:对于
的子集,且满足:对于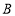 中的任意元素
中的任意元素 、
、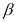 ,当
,当 、
、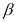 相同时,
相同时,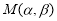 是奇数,当
是奇数,当 、
、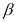 不同时,
不同时,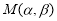 是偶数,求集合
是偶数,求集合 中元素个数的最大值.
中元素个数的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,既是奇函数又是增函数的为( )
A.y=x+1
B.y=﹣x2
C.y=
D.y=x|x|
相关试题

