【题目】如图,在棱长为1正方体![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 所在的直线进行翻折,将
所在的直线进行翻折,将![]() 沿
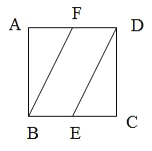
沿![]() 所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
A. 无论旋转到什么位置,![]() 、
、![]() 两点都不可能重合
两点都不可能重合
B. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
C. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
D. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
参考答案:
【答案】D
【解析】
利用圆锥的几何特征逐一判断即可.
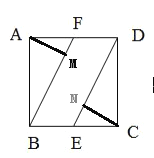
解:过A点作AM⊥BF于M,过C作CN⊥DE于N点
在翻折过程中,AF是以F为顶点,AM为底面半径的圆锥的母线,同理,AB,EC,DC也可以看成圆锥的母线;
在A中,A点轨迹为圆周,C点轨迹为圆周,显然没有公共点,故A正确;
在B中,能否使得直线AF与直线CE所成的角为60°,又AF,EC分别可看成是圆锥的母线,只需看以F为顶点,AM为底面半径的圆锥的轴截面的顶角是否大于等于60°即可,故B正确;
在C中,能否使得直线AF与直线CE所成的角为90°,只需看以F为顶点,AM为底面半径的圆锥的轴截面的顶角是否大于等于90°即可,故C正确;
在D中,能否使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ,只需看以B为顶点,AM为底面半径的圆锥的轴截面的顶角是否大于等于90°即可,故D不成立;
,只需看以B为顶点,AM为底面半径的圆锥的轴截面的顶角是否大于等于90°即可,故D不成立;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中,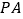 ⊥底面
⊥底面 ,
, 是
是 的中点.
的中点.已知
 ,
, ,
, ,
, .求:
.求:(1)三棱锥PABC的体积;
(2)异面直线BC与AD所成角的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为 ,满足
,满足 .
.(1) 求角
 的大小;
的大小;(2) 若
 ,求
,求 ,
, 的值.(其中
的值.(其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动.为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个小组中随机抽取10名学生参加问卷调查.各组人数统计如下:

(1)从参加问卷调查的10名学生中随机抽取两名,求这两名学生来自同一个小组的概率;
(2)在参加问卷调查的10名学生中,从来自甲、丙两个小组的学生中随机抽取两名,用
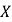 表示抽得甲组学生的人数,求
表示抽得甲组学生的人数,求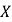 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点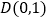 ,且离心率为
,且离心率为 .过抛物线
.过抛物线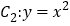 上一点
上一点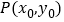 作
作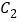 的切线
的切线 交椭圆
交椭圆 于
于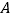 ,
,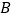 两点.
两点.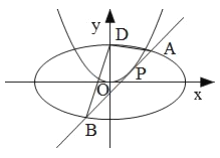
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)是否存在直线
 ,使得
,使得 ,若存在,求出
,若存在,求出 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)若
 ,求证:
,求证: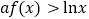 .
.
相关试题

