【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,设
,设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
参考答案:
【答案】(1)  (
(![]() 为参数);(2)
为参数);(2) ![]() .
.
【解析】试题分析:(1)利用直线极坐标方程和直角坐标方程互化的公式,先得直角坐标方程,再根据![]() ,即可求直线l参数方程;(2)把直线l的参数方程代入曲线C的方程,设MP=t1,MQ=t2.根据|PQ|2=|MP||MQ|,
,即可求直线l参数方程;(2)把直线l的参数方程代入曲线C的方程,设MP=t1,MQ=t2.根据|PQ|2=|MP||MQ|, ![]() 根据根与系数的关系即可得出.
根据根与系数的关系即可得出.
解析:(1)直线![]() 的极坐标方程为
的极坐标方程为![]()
所以![]() ,即
,即![]()
因为![]() 为参数,若
为参数,若![]() ,代入上式得
,代入上式得![]() ,
,
所以直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数)
为参数)
(2)由![]() ,得
,得![]()
由![]() 代入,得
代入,得![]()
将直线![]() 的参数方程与
的参数方程与![]() 的直角坐标方程联立
的直角坐标方程联立
得![]() (*)
(*)
![]()
![]() ,
,
设点![]() 分别对应参数
分别对应参数![]() 恰为上述方程的根
恰为上述方程的根
则![]() ,
,
由题设得![]() ,
,
则有![]() ,得
,得![]() 或
或![]()
因为![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:(k﹣1)x﹣2y+5﹣3k=0(k∈R)恒过定点P,圆C经过点A(4,0)和点P,且圆心在直线x﹣2y+1=0上.
(1)求定点P的坐标;
(2)求圆C的方程;
(3)已知点P为圆C直径的一个端点,若另一个端点为点Q,问:在y轴上是否存在一点M(0,m),使得△PMQ为直角三角形,若存在,求出m的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
分组
频数
[2,4)
2
[4,6)
10
[6,8)
16
[8,10)
8
[10,12]
4
合计
40
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.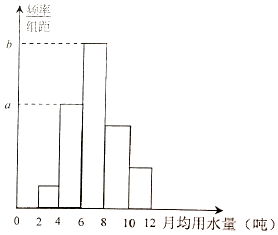
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的斜率为k,经过点(1,﹣1),将直线向右平移3个单位,再向上平移2个单位,得到直线m,若直线m不经过第四象限,则直线l的斜率k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果,在
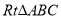 中,
中, 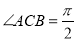 ,
, 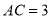 ,
, 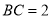 ,
, 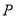 是
是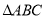 内的一点.
内的一点.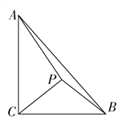
(1)若
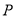 是等腰直角三角形
是等腰直角三角形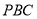 的直角顶点,求
的直角顶点,求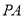 的长;
的长;(2)若
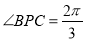 ,设
,设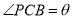 ,求
,求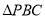 的面积
的面积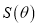 的解析式,并求
的解析式,并求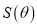 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M:x2+(y﹣2)2=r2(r>0)与曲线C:(y﹣2)(3x﹣4y+3)=0有三个不同的交点.
(1)求圆M的方程;
(2)已知点Q是x轴上的动点,QA,QB分别切圆M于A,B两点. ①若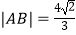 ,求|MQ|及直线MQ的方程;
,求|MQ|及直线MQ的方程;
②求证:直线AB恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
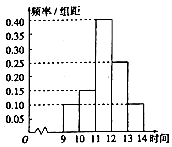
A.100万元
B.10万元
C.7.5万元
D.6.25万元
相关试题

