【题目】如图,在直三棱柱![]() 中,
中, ![]() ,D是棱AC的中点,且
,D是棱AC的中点,且![]() .
.
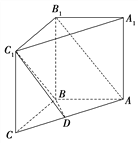
(1)求证: ![]() ;
;
(2)求异面直线![]() 与
与![]() 所成的角.
所成的角.
参考答案:
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:
(1)利用题意结合线面平行的判断定理由OD∥AB1即可证得结论 ;
(2)建立空间直角坐标系,结合题意可得异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.
试题解析:
(1)如图,连接B1C交BC1于点O,连接OD.
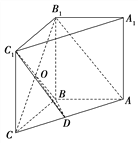
∵O为B1C的中点,D为AC的中点,∴OD∥AB1.
∵AB1平面BC1D,OD平面BC1D,
∴AB1∥平面BC1D.
(2)建立如图所示的空间直角坐标系B-xyz.
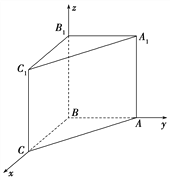
则B(0,0,0)、A(0,2,0)、C1(2,0,2)、B1(0,0,2).
∴![]() =(0,-2,2)、
=(0,-2,2)、![]() =(2,0,2).
=(2,0,2).
cos〈![]() ,
,![]() 〉=
〉=![]()
=![]() =
=![]() ,
,
设异面直线AB1与BC1所成的角为θ,则cosθ=![]() ,
,
∵θ∈(0,![]() ),∴θ=
),∴θ=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若函数
 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;(2)比较
 大小,并写出比较过程;
大小,并写出比较过程;(3)若
 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.(Ⅰ)根据图1,估计乙流水线生产产品该质量指标值的中位数;
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面
 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?甲生产线
乙生产线
合计
合格品
不合格品
合计
附:
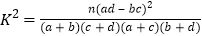 (其中
(其中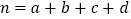 为样本容量)
为样本容量)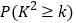
0.15
0.10
0.05
0.025
0.010
0.005
0.001
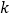
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .
. (1)求
 的值;
的值; (2)求
 的解析式;
的解析式;(3)已知
 ,设
,设 :当
:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足
是单调函数。如果满足 成立的
成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为 ,求A∩(CRB)(
,求A∩(CRB)( 为全集).
为全集). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
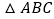 中,角
中,角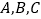 的对边分别为
的对边分别为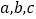 ,
,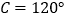 .
.(Ⅰ)若
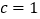 ,求
,求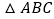 面积的最大值;
面积的最大值;(Ⅱ)若
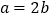 ,求
,求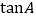 .
.
-
科目: 来源: 题型:
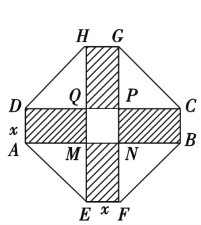
查看答案和解析>>【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
相关试题

