【题目】已知函数![]()
(1)若函数![]() 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较![]() 大小,并写出比较过程;
大小,并写出比较过程;
(3)若![]() ,求a的值.
,求a的值.
参考答案:
【答案】⑴ ![]() . ⑵
. ⑵![]() . ⑶
. ⑶![]() 或
或 ![]() .
.
【解析】本试题主要考查了指数函数的性质的运用。第一问中,因为函数![]() 的图象经过P(3,4)点,所以
的图象经过P(3,4)点,所以![]() ,解得
,解得![]() ,因为
,因为![]() ,所以
,所以![]() .
.
(2)问中,对底数a进行分类讨论,利用单调性求解得到。
(3)中,由![]() 知,
知,![]() .,指对数互化得到
.,指对数互化得到![]() ,,所以
,,所以![]() ,解得所以,
,解得所以,![]() 或
或 ![]() .
.
解:⑴∵函数![]() 的图象经过
的图象经过![]() ∴
∴![]() ,即
,即![]() . … 2分
. … 2分
又![]() ,所以
,所以![]() . ………… 4分
. ………… 4分
⑵当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() . ……………… 6分
. ……………… 6分
因为,![]() ,
,![]()
当![]() 时,
时,![]() 在
在![]() 上为增函数,∵
上为增函数,∵![]() ,∴
,∴![]() .
.
即![]() .当
.当![]() 时,
时,![]() 在
在![]() 上为减函数,
上为减函数,
∵![]() ,∴
,∴![]() .即
.即![]() . …………………… 8分
. …………………… 8分
⑶由![]() 知,
知,![]() .所以,
.所以,![]() (或
(或![]() ).
).
∴![]() .∴
.∴![]() , … 10分
, … 10分
∴![]() 或
或 ![]() ,所以,
,所以,![]() 或
或 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 是奇函数,且f(2)=
是奇函数,且f(2)= .
.(1)求实数m和n的值;
(2)判断函数f(x)在(-∞,0)上的单调性,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:极坐标与参数方程
在平面直角坐标系
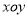 中,直线
中,直线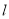 的参数方程为:
的参数方程为: 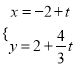 (t为参数),它与曲线C:
(t为参数),它与曲线C: 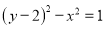 相交于A,B两点.
相交于A,B两点.(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为
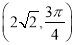 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①
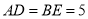 ;②当
;②当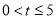 时,
时, 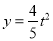 ;③
;③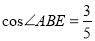 ;④当
;④当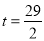 秒时,
秒时,  ∽
∽ ;⑤当
;⑤当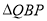 的面积为
的面积为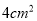 时,时间
时,时间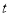 的值是
的值是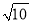 或
或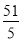 ;其中正确的结论是( )
;其中正确的结论是( )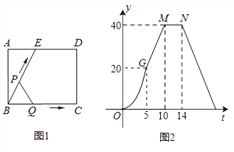
A. ①⑤ B. ②⑤ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.(Ⅰ)根据图1,估计乙流水线生产产品该质量指标值的中位数;
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面
 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?甲生产线
乙生产线
合计
合格品
不合格品
合计
附:
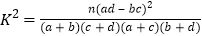 (其中
(其中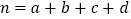 为样本容量)
为样本容量)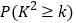
0.15
0.10
0.05
0.025
0.010
0.005
0.001
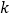
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
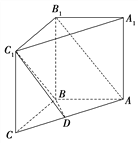
查看答案和解析>>【题目】如图,在直三棱柱
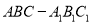 中,
中, 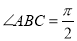 ,D是棱AC的中点,且
,D是棱AC的中点,且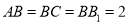 .
.
(1)求证:
 ;
;(2)求异面直线
 与
与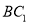 所成的角.
所成的角.
相关试题

