【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
(Ⅰ)根据图1,估计乙流水线生产产品该质量指标值的中位数;
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() ;(III)没有85%的把握认为“该企业生产的这种产品的该项质量指标值与甲,乙两条流水线的选择有关”.
;(III)没有85%的把握认为“该企业生产的这种产品的该项质量指标值与甲,乙两条流水线的选择有关”.
【解析】试题分析:(I)由频率分步直方图,结合中位数定义,可利用面积进行计算,中位数所在位置将所有小矩形的面积一分为二;(II)由频率知概率,已知样本容量,可利用概率求得甲乙产品合格,不合格的个数;(III)由列联表可求得![]() 值,查表可得对应概率.
值,查表可得对应概率.
试题解析:
(Ⅰ)设乙流水线生产产品的该项质量指标值的中位数为![]() ,因为
,因为
![]() 则
则![]() 解得
解得![]() .
.
(Ⅱ)由甲,乙两条流水线各抽取的50件产品可得,甲流水线生产的不合格品有15件, 则甲流水线生产的产品为不合格品的概率为![]() 乙流水线生产的产品为不合格品的概率为
乙流水线生产的产品为不合格品的概率为![]() , 于是,若某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线生产的不合格品件数分别为:
, 于是,若某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线生产的不合格品件数分别为:
![]() .
.
(Ⅲ)![]() 列联表:
列联表:
甲生产线 | 乙生产线 | 合计 | |
合格品 | 35 | 40 | 75 |
不合格品 | 15 | 10 | 25 |
合计 | 50 | 50 | 100 |
则![]() ,
,
因为![]()
所以没有85%的把握认为“该企业生产的这种产品的该项质量指标值与甲,乙两条流水线 的选择有关”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①
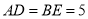 ;②当
;②当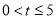 时,
时, 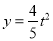 ;③
;③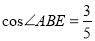 ;④当
;④当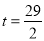 秒时,
秒时,  ∽
∽ ;⑤当
;⑤当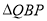 的面积为
的面积为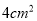 时,时间
时,时间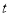 的值是
的值是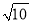 或
或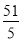 ;其中正确的结论是( )
;其中正确的结论是( )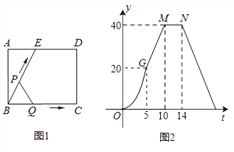
A. ①⑤ B. ②⑤ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若函数
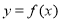 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;(2)比较
 大小,并写出比较过程;
大小,并写出比较过程;(3)若
 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
-
科目: 来源: 题型:
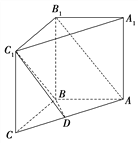
查看答案和解析>>【题目】如图,在直三棱柱
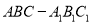 中,
中, 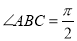 ,D是棱AC的中点,且
,D是棱AC的中点,且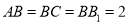 .
.
(1)求证:
 ;
;(2)求异面直线
 与
与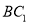 所成的角.
所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .
. (1)求
 的值;
的值; (2)求
 的解析式;
的解析式;(3)已知
 ,设
,设 :当
:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足
是单调函数。如果满足 成立的
成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为 ,求A∩(CRB)(
,求A∩(CRB)( 为全集).
为全集). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
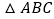 中,角
中,角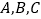 的对边分别为
的对边分别为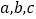 ,
,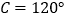 .
.(Ⅰ)若
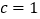 ,求
,求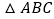 面积的最大值;
面积的最大值;(Ⅱ)若
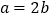 ,求
,求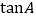 .
.
相关试题

