【题目】已知定义在R上的函数y=f(x)对于任意的x都满足f(x+1)=-f(x),当-1≤x<1时,f(x)=x3,若函数g(x)=f(x)-loga|x|至少有6个零点,则a的取值范围是( )
A. ![]() ∪(5,+∞) B.
∪(5,+∞) B. ![]() ∪
∪![]()
C. ![]() ∪(5,7) D.
∪(5,7) D. ![]() ∪[5,7)
∪[5,7)
参考答案:
【答案】A
【解析】由f(x+1)=-f(x)得f(x+1)=-f(x+2),
因此f(x)=f(x+2),即函数f(x)是周期为2的周期函数.
函数g(x)=f(x)-loga|x|至少有6个零点可转化成y=f(x)与h(x)=loga|x|两函数图象交点至少有6个,需对底数a进行分类讨论.若a>1,则h(5)=loga5<1,即a>5.
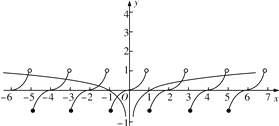
若0<a<1,则h(-5)=loga5≥-1,即0<a≤![]() .
.
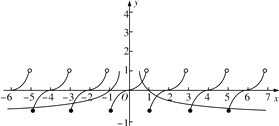
所以a的取值范围是![]() ∪(5,+∞).故选A.
∪(5,+∞).故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知国家某5A级大型景区对拥挤等级与每日游客数量
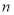 (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当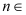
 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当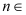
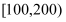 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当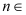
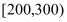 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当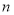
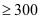 时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据: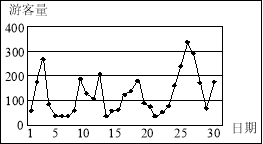
(Ⅰ)下面是根据统计数据得到的频率分布表,求出
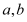 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);游客数量
(单位:百人)

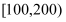
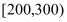
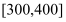
天数
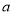

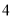
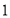
频率
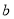
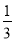
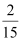
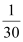
(Ⅱ)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年的蔬菜销售收入均为50万元,设
 表示前
表示前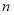 年的纯利润总和(
年的纯利润总和(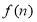 =前
=前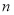 年的总收入
年的总收入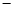 前
前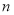 年的总支出
年的总支出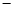 投资额).
投资额).(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:
① 当年平均利润达到最大时,以48万元出售该厂;
② 当纯利润总和达到最大时,以16万元出售该厂,
问哪种方案更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把离心率
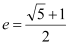 的双曲线
的双曲线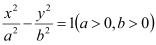 称为黄金双曲线.给出以下几个说法:
称为黄金双曲线.给出以下几个说法:①双曲线
 是黄金双曲线;
是黄金双曲线;②若双曲线上一点
 到两条渐近线的距离积等于
到两条渐近线的距离积等于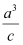 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;③若
 为左右焦点,
为左右焦点, 为左右顶点,
为左右顶点, 且
且 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;④.若直线
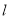 经过右焦点
经过右焦点 交双曲线于
交双曲线于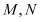 两点,且
两点,且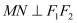 ,
,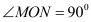 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;其中正确命题的序号为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)当
 时,证明:对任意的
时,证明:对任意的 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
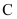 的中心为坐标原点,其离心率为
的中心为坐标原点,其离心率为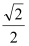 ,椭圆
,椭圆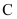 的一个焦点和抛物线
的一个焦点和抛物线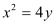 的焦点重合.
的焦点重合.(1)求椭圆
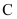 的方程
的方程
(2)过点
 的动直线
的动直线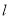 交椭圆
交椭圆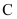 于
于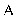 、
、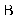 两点,试问:在平面上是否存在一个定点
两点,试问:在平面上是否存在一个定点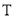 ,使得无论
,使得无论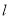 如何转动,以
如何转动,以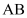 为直径的圆恒过点
为直径的圆恒过点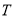 ,若存在,说出点
,若存在,说出点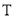 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】动点
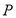 在抛物线
在抛物线 上,过点
上,过点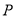 作
作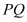 垂直于
垂直于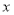 轴,垂足为
轴,垂足为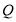 ,设
,设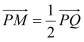 .
.(Ⅰ)求点
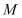 的轨迹
的轨迹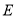 的方程;
的方程;(Ⅱ)设点
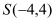 ,过点
,过点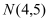 的直线
的直线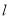 交轨迹
交轨迹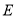 于
于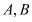 两点,直线
两点,直线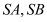 的斜率分别为
的斜率分别为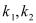 ,求
,求 的最小值.
的最小值.
相关试题

