【题目】已知函数![]() ,
,
(1)当![]() 时,证明:函数
时,证明:函数![]() 不是奇函数;
不是奇函数;
(2)判断函数![]() 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;
(3)若![]() 是奇函数,且
是奇函数,且![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)当![]() 时,
时,![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 不是奇函数; ……………………………………4分
不是奇函数; ……………………………………4分
(Ⅱ)函数![]() 在
在![]() 上为单调增函数, ………………………………………… 6分
上为单调增函数, ………………………………………… 6分
证明:设![]() ,则
,则![]() ……… 8分
……… 8分
∵![]() ,∴
,∴![]() ,
,![]() ,且
,且![]()
又∵![]() ,∴
,∴![]()
∴![]() ,故
,故![]() 。
。
∴函数![]() 在
在![]() 上为单调增函数。…………………………………………………10分
上为单调增函数。…………………………………………………10分
(Ⅲ)因为![]() 是奇函数,所以
是奇函数,所以![]() 对任意
对任意![]() 恒成立。
恒成立。
即![]() 对任意
对任意![]() 恒成立.
恒成立.
化简整理得![]() 对任意
对任意![]() 恒成立. ∴
恒成立. ∴![]() …………………12分
…………………12分
又因为![]() 在
在![]() 时恒成立,
时恒成立,
所以![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,设
,设![]() ,且
,且![]() ,
,
则![]()
由(Ⅱ)可知,![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,
,
故函数![]() 在
在![]() 上是增函数。………………………14分
上是增函数。………………………14分
所以![]() ,由
,由![]()
![]() 。
。
因此![]() 的取值范围是
的取值范围是![]() 。 ………………………………………………16分
。 ………………………………………………16分
【解析】试题分析:(1)举个反例,使得f(-a)≠-f(a)即可;(2)利用函数的单调性进行证明即可,注意指数函数y=2x性质的运用;(3)先根据题意求出a的值,然后f(x)≥x2-4x+m在x∈[-2,2]时恒成立,将式子变形为f(x)-(x2-4x)≥m在x∈[-2,2]时恒成立即可,在研究左边函数的单调性,求出其最小值即可
试题解析:(1)当![]() 时,
时,![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 不是奇函数;
不是奇函数;
(2)函数![]() 在
在![]() 上为单调增函数,
上为单调增函数,
证明:设![]() ,则
,则![]()
∵![]() ,∴
,∴![]() ,
,![]() ,且
,且![]()
又∵![]() ,∴
,∴![]()
∴![]() ,故
,故![]()
∴函数![]() 在
在![]() 上为单调增函数
上为单调增函数
(3)因为![]() 是奇函数,所以
是奇函数,所以![]() 对任意
对任意![]() 恒成立。
恒成立。
即![]() 对任意
对任意![]() 恒成立.
恒成立.
化简整理得![]() 对任意
对任意![]() 恒成立. ∴
恒成立. ∴![]()
因为![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,设
,设![]() ,且
,且![]() ,
,
则![]()
由(2)可知,![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,
,
故函数![]() 在
在![]() 上是增函数 (直接判断出单调性也给分)
上是增函数 (直接判断出单调性也给分)
所以![]() ,由
,由![]()
![]()
因此![]() 的取值范围是
的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
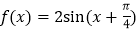
(1)用“五点法”作出函数
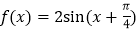 在一个周期内的简图;
在一个周期内的简图;(2)求出函数的最大值及取得最大值时的x的值;
(3)求出函数在
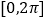 上的单调区间.
上的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
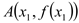 ,
,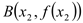 是函数
是函数
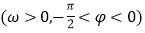 图象上的任意两点,且角
图象上的任意两点,且角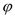 的终边经过点
的终边经过点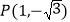 ,若
,若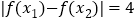 时,
时,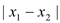 的 最小值为
的 最小值为 .
.(1)求函数
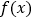 的解析式;
的解析式;(2)当
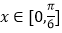 时,不等式
时,不等式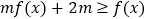 恒成立,求实数
恒成立,求实数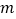 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
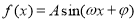
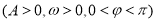 ,若函数
,若函数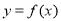 的图象与x轴的任意两个相邻交点间的距离为
的图象与x轴的任意两个相邻交点间的距离为 ,当
,当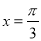 时,函数
时,函数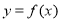 取得最大值
取得最大值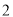 .
.(1)求函数
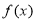 的解析式,并写出它的单调增区间;
的解析式,并写出它的单调增区间;(2)若
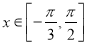 ,求函数
,求函数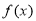 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知动直线
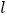 过点
过点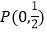 ,且与圆
,且与圆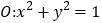 交于
交于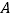 、
、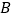 两点.
两点.(1)若直线
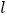 的斜率为
的斜率为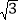 ,求
,求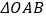 的面积;
的面积;(2)若直线
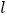 的斜率为
的斜率为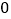 ,点
,点 是圆
是圆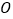 上任意一点,求
上任意一点,求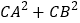 的取值范围;
的取值范围;(3)是否存在一个定点
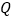 (不同于点
(不同于点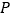 ),对于任意不与
),对于任意不与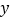 轴重合的直线
轴重合的直线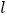 ,都有
,都有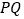 平分
平分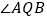 ,若存在,求出定点
,若存在,求出定点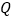 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.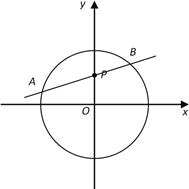
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,设
,设 ,
, ,其中
,其中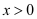 ,
,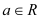 .
.(1)若函数
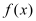 在区间
在区间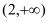 上单调递增,求实数
上单调递增,求实数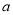 的取值范围;
的取值范围;(2)记
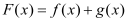 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了普及法律知识,达到“法在心中”的目的,某市法制办组织了普法知识竞赛.统计局调查队随机抽取了甲、乙两单位中各5名职工的成绩,成绩如下表:
甲单位
87
88
91
91
93
乙单位
85
89
91
92
93
(1)根据表中的数据,分别求出甲、乙两单位职工成绩的平均数和方差,并判断哪个单位对法律知识的掌握更稳定;
(2)用简单随机抽样法从乙单位5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的分数差至少是4的概率.
相关试题

