【题目】为了普及法律知识,达到“法在心中”的目的,某市法制办组织了普法知识竞赛.统计局调查队随机抽取了甲、乙两单位中各5名职工的成绩,成绩如下表:
甲单位 | 87 | 88 | 91 | 91 | 93 |
乙单位 | 85 | 89 | 91 | 92 | 93 |
(1)根据表中的数据,分别求出甲、乙两单位职工成绩的平均数和方差,并判断哪个单位对法律知识的掌握更稳定;
(2)用简单随机抽样法从乙单位5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的分数差至少是4的概率.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ,甲单位对法律知识的掌握更稳定;(2)
,甲单位对法律知识的掌握更稳定;(2)![]() .
.
【解析】
试题分析:(1)先求出甲乙两个单位职工的考试成绩的平均数,以及他们的方差,则方差小的更稳定;(2)从乙单位抽取两名职工的成绩,所有基本事件用列举法得到共![]() 种情况,抽取的两名职工的分数差至少是
种情况,抽取的两名职工的分数差至少是![]() 的事件用列举法求得共有
的事件用列举法求得共有![]() 种,由古典概型公式得出概率.
种,由古典概型公式得出概率.
试题解析:解:(1)![]() ,
,![]()
![]()
![]()
∵![]() ,∴甲单位的成绩比乙单位稳定,即甲单位对法律知识的掌握更稳定.
,∴甲单位的成绩比乙单位稳定,即甲单位对法律知识的掌握更稳定.
(2)从乙单位5名职工中抽取2名,他们的成绩组成的所有基本事件(用数对表示):(85,89),(85,91),(85,92),(85,93),(89,91),(89,92),(89,93),(91,92),(91,93),(92,93),共10个.
则抽取的2名职工的分数差至少是4的基本事件:
(85,89),(85,91),(85,92),(85,93),(89,93),
共5个.
用古典概型的概率计算公式可知,抽取的2名职工的分数差至少是4的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
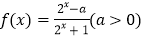 ,
,(1)当
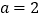 时,证明:函数
时,证明:函数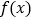 不是奇函数;
不是奇函数;(2)判断函数
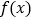 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;(3)若
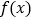 是奇函数,且
是奇函数,且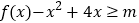 在
在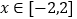 时恒成立,求实数
时恒成立,求实数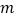 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知动直线
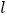 过点
过点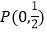 ,且与圆
,且与圆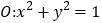 交于
交于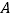 、
、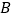 两点.
两点.(1)若直线
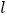 的斜率为
的斜率为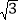 ,求
,求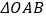 的面积;
的面积;(2)若直线
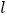 的斜率为
的斜率为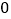 ,点
,点 是圆
是圆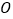 上任意一点,求
上任意一点,求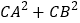 的取值范围;
的取值范围;(3)是否存在一个定点
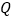 (不同于点
(不同于点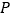 ),对于任意不与
),对于任意不与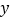 轴重合的直线
轴重合的直线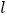 ,都有
,都有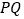 平分
平分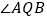 ,若存在,求出定点
,若存在,求出定点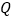 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.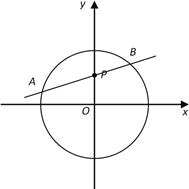
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,设
,设 ,
, ,其中
,其中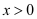 ,
,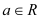 .
.(1)若函数
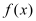 在区间
在区间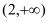 上单调递增,求实数
上单调递增,求实数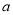 的取值范围;
的取值范围;(2)记
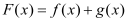 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
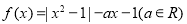 .
.(1)若关于
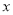 的方程
的方程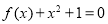 在区间
在区间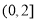 上有两个不同的解
上有两个不同的解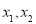 .
.(ⅰ)求
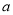 的取值范围;
的取值范围;(ⅱ)若
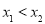 ,求
,求 的取值范围;
的取值范围;(2)设函数
 在区间
在区间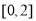 上的最大值和最小值分别为
上的最大值和最小值分别为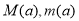 ,求
,求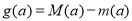 的表达式.
的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
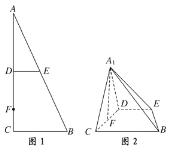
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
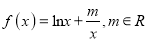 .
.(1)当
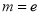 (
(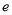 为自然对数的底数)时,求
为自然对数的底数)时,求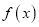 的最小值;
的最小值;(2)讨论函数
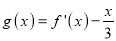 零点的个数;
零点的个数;(3)若对任意
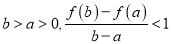 恒成立,求
恒成立,求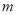 的取值范围.
的取值范围.
相关试题

