【题目】已知函数![]()
(1)用“五点法”作出函数![]() 在一个周期内的简图;
在一个周期内的简图;
(2)求出函数的最大值及取得最大值时的x的值;
(3)求出函数在![]() 上的单调区间.
上的单调区间.
参考答案:
【答案】(1)见解析;(2)当![]() ,k∈Z时,函数的最大值为2;(3)函数在[0,2π]上的单调递减区间为
,k∈Z时,函数的最大值为2;(3)函数在[0,2π]上的单调递减区间为![]()
【解析】试题分析:(1)令![]() 分别等于
分别等于![]() 可得五点的横坐标,求出对应的
可得五点的横坐标,求出对应的![]() 值,描点、作图即可;(2)由
值,描点、作图即可;(2)由![]()
![]() ,可得取得最大值时的x的值;(3)利用正弦定理的单调增区间,可求函数
,可得取得最大值时的x的值;(3)利用正弦定理的单调增区间,可求函数![]() 的单调增区间与
的单调增区间与![]() 求交集即可得结果.
求交集即可得结果.
试题解析:(1)列表如下:
x ﹣![]()
![]()
![]()
![]()
![]()
x+![]() 0
0 ![]() π
π ![]() 2π
2π
2sin(x+![]() ) 0 2 0 ﹣2 0
) 0 2 0 ﹣2 0
描点、连线,得图.

(2)由图可知:当x=![]() +2kπ,k∈Z时,函数的最大值为2.
+2kπ,k∈Z时,函数的最大值为2.
(3)由图可知:函数在[0,2π]上的单调递增区间为
[0,![]() ]和[
]和[![]() ,2π],
,2π],
函数在[0,2π]上的单调递减区间为[![]() ,
,![]() ].
].
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 的左、右焦点分别为
的左、右焦点分别为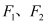 ,过点
,过点 作垂直于
作垂直于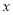 轴的直线
轴的直线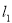 ,直线
,直线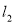 垂直
垂直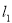 于点
于点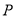 ,线段
,线段 的垂直平分线交
的垂直平分线交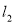 于点
于点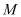 .
.(1)求点
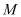 的轨迹
的轨迹 的方程;
的方程;(2)过点
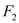 作两条互相垂直的直线
作两条互相垂直的直线 ,且分别交椭圆于
,且分别交椭圆于 ,求四边形
,求四边形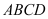 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体
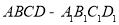 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段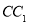 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。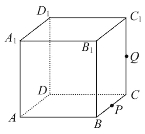
①当
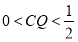 时,S为四边形
时,S为四边形②当
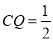 时,S为等腰梯形
时,S为等腰梯形③当
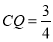 时,S与
时,S与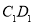 的交点R满足
的交点R满足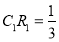
④当
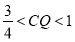 时,S为六边形
时,S为六边形⑤当
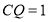 时,S的面积为
时,S的面积为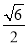
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .
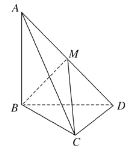
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
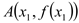 ,
,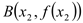 是函数
是函数
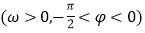 图象上的任意两点,且角
图象上的任意两点,且角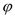 的终边经过点
的终边经过点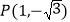 ,若
,若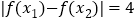 时,
时,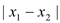 的 最小值为
的 最小值为 .
.(1)求函数
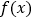 的解析式;
的解析式;(2)当
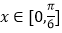 时,不等式
时,不等式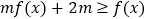 恒成立,求实数
恒成立,求实数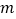 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
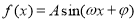
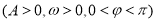 ,若函数
,若函数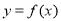 的图象与x轴的任意两个相邻交点间的距离为
的图象与x轴的任意两个相邻交点间的距离为 ,当
,当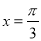 时,函数
时,函数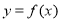 取得最大值
取得最大值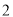 .
.(1)求函数
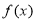 的解析式,并写出它的单调增区间;
的解析式,并写出它的单调增区间;(2)若
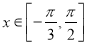 ,求函数
,求函数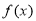 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
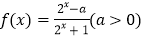 ,
,(1)当
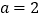 时,证明:函数
时,证明:函数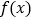 不是奇函数;
不是奇函数;(2)判断函数
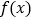 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;(3)若
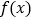 是奇函数,且
是奇函数,且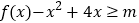 在
在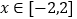 时恒成立,求实数
时恒成立,求实数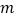 的取值范围.
的取值范围.
相关试题

