【题目】某地区有小学21所,中学14所,现采用分层抽样的方法从这些学校中抽取5所学校,对学生进行视力检查.
(1)求应从小学、中学中分别抽取的学校数目;
(2)若从抽取的5所学校中抽取2所学校作进一步数据
①列出所有可能抽取的结果;
②求抽取的2所学校至少有一所中学的概率.
参考答案:
【答案】(1)3所、2所;(2)①![]() 共10种 ;
共10种 ;
②![]()
【解析】
(1)根据分层抽样的方法,得到分层抽样的比例,即可求解样本中小学与中学抽取的学校数目;
(2)①3所小学分别记为![]() ;2所中学分别记为
;2所中学分别记为![]() ,利用列举法,即可求得抽取的2所学校的所有结果;
,利用列举法,即可求得抽取的2所学校的所有结果;
②利用古典概型的概率计算公式,即可求得相应的概率.
(1)学校总数为35所,所以分层抽样的比例为![]() ,
,
计算各类学校应抽取的数目为:![]() ,
,
故从小学、中学中分别抽取的学校数目为3所、2所.
(2)①3所小学分别记为![]() ;2所中学分别记为
;2所中学分别记为![]()
应抽取的2所学校的所有结果为:![]()
![]() 共10种.
共10种.
②设“抽取的2所学校至少有一所中学”作为事件![]() .
.
其结果共有7种,所以概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:
 )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间 ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量
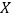 (单位:瓶)的分布列;
(单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为
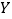 (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量 (单位:瓶)为多少时,
(单位:瓶)为多少时,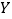 的数学期望达到最大值?
的数学期望达到最大值? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足sin2B+sin2C=sin2A+2sinBsinCsin(B+C). (Ⅰ)求角A的大小;
(Ⅱ)若a=2,求△ABC面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x∈R|x2+4x=0},B={x∈R|x2+2(a+1)x+a2-1=0,a∈R},若BA,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆

(1)求圆
 关于直线
关于直线 对称的圆
对称的圆 的标准方程;
的标准方程;(2)过点
 的直线
的直线 被圆
被圆 截得的弦长为8,求直线
截得的弦长为8,求直线 的方程;
的方程;(3)当
 取何值时,直线
取何值时,直线 与圆
与圆 相交的弦长最短,并求出最短弦长.
相交的弦长最短,并求出最短弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,函数
,函数 .
.(1)当
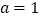 时,求
时,求 在
在 上的单调区间;
上的单调区间;(2)设函数
 ,当
,当 有两个极值点
有两个极值点 时,总有
时,总有 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所发现,一中作物的年收获量y(单位:kg)与它”相近“作物的株数x具有线性相关关系(所谓两株作物”相近“是指它们的直线距离不超过1m),并分别记录了相近作物的株数为1,2,3,5,6,7时,该作物的年收获量的相关数据如下:
X
1
2
3
5
6
7
y
60
55
53
46
45
41

(Ⅰ)求该作物的年收获量y关于它”相近“作物的株数x的线性回归方程;
(Ⅱ)农科所在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每一个小正方形的面积为1,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以线性回归方程计算所得数据为依据)
附:对于一组数据(x1 , y1),(x2 , y2),…,(xn , yn),其回归直线y=a+bx的斜率和截距的最小二乘估计分别为 =
=  =
=  ,
,  =
=  ﹣
﹣  .
.
相关试题

