【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足sin2B+sin2C=sin2A+2sinBsinCsin(B+C). (Ⅰ)求角A的大小;
(Ⅱ)若a=2,求△ABC面积的最大值.
参考答案:
【答案】解:(Ⅰ)sin2B+sin2C=sin2A+2sinBsinCsin(B+C), 由正弦定理可得 b2+c2=a2+2bcsinA,
由余弦定理可得 b2+c2﹣a2=2bcsinA,
∴cosA=sinA,
∴tanA=1,
∵A∈(0,π),
∴A= ![]()
(Ⅱ)由(Ⅰ)可得b2+c2=4+ ![]() bc,
bc,
∵b2+c2≥2bc,
∴4+ ![]() bc≥2bc,当且仅当b=c时取等号,
bc≥2bc,当且仅当b=c时取等号,
即bc≤ ![]() =4+2
=4+2 ![]() ,
,
∴S△ABC= ![]() bcsinA=
bcsinA= ![]() bc≤
bc≤ ![]() +1,
+1,
∴△ABC面积的最大值 ![]() +1.
+1.
【解析】(1)由条件利用正弦定理可得 b2+c2=a2+2bcsinA,再由余弦定理可得cosA=sinA,即可求出A,(Ⅱ)根据基本不等式求出bc≤4+2 ![]() ,再根据三角形的面积公式计算即可
,再根据三角形的面积公式计算即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 的方程为
的方程为 ,过点
,过点 的直线
的直线 与圆
与圆 交于两点
交于两点 ,
, .
.(1)若
 ,求直线
,求直线 的方程;
的方程;(2)若直线
 与
与 轴交于点
轴交于点 ,设
,设 ,
, ,
,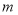 ,
, R,求
R,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,anan+1=2Sn , 设bn=
 ,若存在正整数p,q(p<q),使得b1 , bp , bq成等差数列,则p+q= .
,若存在正整数p,q(p<q),使得b1 , bp , bq成等差数列,则p+q= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:
 )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间 ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量
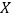 (单位:瓶)的分布列;
(单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为
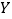 (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量 (单位:瓶)为多少时,
(单位:瓶)为多少时,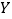 的数学期望达到最大值?
的数学期望达到最大值? -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x∈R|x2+4x=0},B={x∈R|x2+2(a+1)x+a2-1=0,a∈R},若BA,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有小学21所,中学14所,现采用分层抽样的方法从这些学校中抽取5所学校,对学生进行视力检查.
(1)求应从小学、中学中分别抽取的学校数目;
(2)若从抽取的5所学校中抽取2所学校作进一步数据
①列出所有可能抽取的结果;
②求抽取的2所学校至少有一所中学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆

(1)求圆
 关于直线
关于直线 对称的圆
对称的圆 的标准方程;
的标准方程;(2)过点
 的直线
的直线 被圆
被圆 截得的弦长为8,求直线
截得的弦长为8,求直线 的方程;
的方程;(3)当
 取何值时,直线
取何值时,直线 与圆
与圆 相交的弦长最短,并求出最短弦长.
相交的弦长最短,并求出最短弦长.
相关试题

