【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 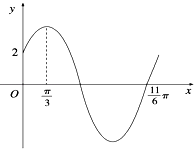
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
(3)当x∈[﹣ ![]() ,
, ![]() ]时,求函数y=f(x+
]时,求函数y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )的最值.
)的最值.
参考答案:
【答案】
(1)解:由图可得, ![]() ,
,
∴T=2π,则 ![]() .
.
由五点作图的第二点知, ![]() φ=
φ= ![]() ,则φ=
,则φ= ![]() .
.
∴f(x)=Asin(x+ ![]() ),
),
又f(0)=Asin ![]() =2,得A=4.
=2,得A=4.
∴f(x)=4sin(x+ ![]() )
)
(2)解:将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍所得函数解析式
倍所得函数解析式
为y=4sin(2x+ ![]() ),再将所得函数图象向右平移
),再将所得函数图象向右平移 ![]() 个单位,解析式变为y=4sin[2(x﹣
个单位,解析式变为y=4sin[2(x﹣ ![]() )+
)+ ![]() ],
],
∴g(x)=4sin(2x﹣ ![]() ).
).
由 ![]() ,解得:
,解得: ![]() .
.
∴g(x)的单调递增区间为 ![]()
(3)解:y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )
)
=4sin(x+ ![]() +
+ ![]() )﹣4
)﹣4 ![]() sin(x+
sin(x+ ![]() +
+ ![]() )
)
=4sin(x+ ![]() )﹣4
)﹣4 ![]() cosx
cosx
=4sinxcos ![]() +4cosxsin
+4cosxsin ![]() ﹣
﹣ ![]()
=4sin(x﹣ ![]() ).
).
∵x∈[﹣ ![]() ,
, ![]() ],
],
∴ ![]() ,
,
∴函数y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )的最小值为﹣4,最大值为2.
)的最小值为﹣4,最大值为2.
【解析】(1)由图得到函数的四分之三周期,进一步求得周期,代入周期公式求ω,然后利用五点作图的第二点求得φ,再由f(0)=2求得A的值,则函数解析式可求;(2)由函数的周期变化和平移变换求得g(x),然后再由简单的复合函数单调性的求法求解g(x)的增区间;(3)结合(1)中的f(x)的解析式求得y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() ),利用三角恒等变换变形后根据x的范围求最值.
),利用三角恒等变换变形后根据x的范围求最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点、焦点在x轴上的椭圆,它的离心率为
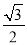 ,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.
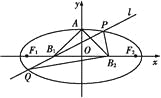
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知sinα+cosα=
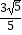 ,α∈(0,
,α∈(0,  ),sin(β﹣
),sin(β﹣  )=
)= 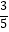 ,β∈(
,β∈(  ,
,  ).
).
(1)求sin2α和tan2α的值;
(2)求cos(α+2β)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(cos
=(cos  x,sin
x,sin  x),
x),  =(cos
=(cos  x,﹣sin
x,﹣sin  x),且x∈[0,
x),且x∈[0,  ].求:
].求:
(1) 及
及  ;
;
(2)若f(x)= ﹣2λ
﹣2λ  的最小值是﹣
的最小值是﹣  ,求λ的值.
,求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
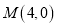 ,
, 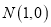 ,曲线
,曲线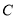 上的任意一点
上的任意一点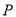 满足:
满足: 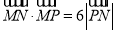 .
.(1)求点
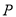 的轨迹方程;
的轨迹方程;(2)过点
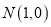 的直线与曲线
的直线与曲线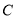 交于
交于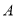 ,
, 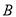 两点,交
两点,交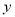 轴于
轴于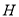 点,设
点,设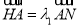 ,
, 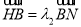 ,试问
,试问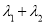 是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( )
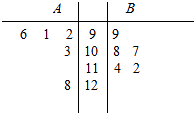
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定
相关试题

