【题目】定义在![]() 上的函数
上的函数![]() ,若已知其在
,若已知其在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时函数取得最大值为
时函数取得最大值为![]() ;当
;当![]() ,函数取得最小值为
,函数取得最小值为![]() .
.
(1)求出此函数的解析式;
(2)若将函数![]() 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的![]() 得到函数
得到函数![]() ,再将函数
,再将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() ,已知函数
,已知函数![]() 的最大值为
的最大值为![]() ,求满足条件的
,求满足条件的![]() 的最小值;
的最小值;
(3)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值),若不存在,请说明理由.
的范围(或值),若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)利用最大值和最小值确定![]() 和
和![]() ,进而得到
,进而得到![]() ;利用
;利用![]() 可求得
可求得![]() 的取值,进而得到所求函数解析式;
的取值,进而得到所求函数解析式;
(2)由图象平移和伸缩变换原则得到![]() ,由
,由![]() 与函数
与函数![]() 的单调性可知只有当
的单调性可知只有当![]() ,
,![]() 同时取得时,函数取最大值,由此可得到
同时取得时,函数取最大值,由此可得到![]() ,根据
,根据![]() 得到最终结果;
得到最终结果;
(3)由偶次根式被开方数大于等于零可确定![]() 的范围,进而得到两角整体所处范围,根据函数单调性可得到
的范围,进而得到两角整体所处范围,根据函数单调性可得到![]() ,解不等式即可求得结果.
,解不等式即可求得结果.
(1)![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
解得:![]() ,
,![]() ,又
,又![]()
![]()
![]()
(2)由题意知:![]() ,
,![]()
![]() 函数
函数![]() 与函数
与函数![]() 均为单调增函数,且
均为单调增函数,且![]() ,
,![]()
![]() 当且仅当
当且仅当![]() 与
与![]() 同时取得才有函数的最大值为
同时取得才有函数的最大值为![]()
由![]() 得:
得:![]() ,
,![]()
又![]()
![]()
![]() ,
,![]()
又![]()
![]() 的最小值为
的最小值为![]()
(3)![]() 满足
满足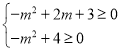 ,解得:
,解得:
![]()
![]()
同理![]()
![]() ,
,![]()
![]() ,
,![]()
由(1)知函数在![]() 上递增
上递增
若有![]()
只需要:![]() ,即
,即![]() 成立即可
成立即可
![]() 存在
存在![]() ,使
,使![]() 成立
成立
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为定义在
为定义在 上的奇函数,且当
上的奇函数,且当 时,
时,
(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)求函数
 在区间
在区间  上的最小值.
上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】由
 可组成不同的四位数的个数为__________.
可组成不同的四位数的个数为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.
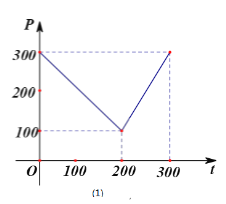
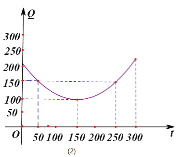
(1)写出图(1)表示的市场售价与时间的函数关系式
 ;写出图(2)表示的种植成本与时间的函数关系式
;写出图(2)表示的种植成本与时间的函数关系式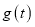 ;
;(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/
 kg,时间单位:天.)
kg,时间单位:天.) -
科目: 来源: 题型:
查看答案和解析>>【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取
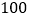 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.表1
停车距离
 (米)
(米)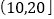

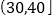
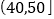

频数
24
42
24
9
1
表2
平均每毫升血液酒精含量
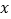 毫克
毫克10
30
50
70
90
平均停车距离
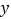 米
米30
50
60
70
90
回答以下问题.
(1)由表1估计驾驶员无酒状态下停车距离的平均数;
(2)根据最小二乘法,由表2的数据计算
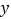 关于
关于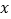 的回归方程
的回归方程 ;
;(3)该测试团队认为:驾驶员酒后驾车的平均“停车距离”
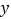 大于(1)中无酒状态下的停车距离平均数的
大于(1)中无酒状态下的停车距离平均数的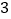 倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)(附:对于一组数据
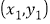 ,
,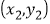 ,…,
,…,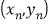 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为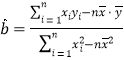 ,
,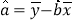 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四种说法:
(1)函数
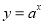
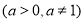 与函数
与函数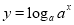
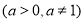 的定义域相同;
的定义域相同;(2)函数
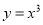 与
与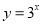 的值域相同;
的值域相同;(3)若函数
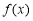 式定义在R上的偶函数且在
式定义在R上的偶函数且在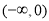 为减函数对于锐角
为减函数对于锐角 则
则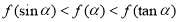 ;
;(4)若函数
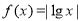 且
且
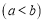 ,则
,则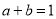 ;
;其中正确说法的序号是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱柱
 ,平面
,平面 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)证明:
 ;
;(2)求直线
 与平面
与平面 所成角的余弦值.
所成角的余弦值.
相关试题

