【题目】已知椭圆![]() 的两个焦点与短轴的一个顶点构成底边为
的两个焦点与短轴的一个顶点构成底边为![]() ,顶角为
,顶角为![]() 的等腰三角形.
的等腰三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 、
、![]() 、
、![]() 是椭圆上三动点,且
是椭圆上三动点,且![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)两个焦点与短轴的一个顶点构成底边为![]() ,顶角为
,顶角为![]() 的等腰三角形.说明
的等腰三角形.说明![]() ,再由直角三角形得
,再由直角三角形得![]() ,从而可得
,从而可得![]() 值,得标准方程;
值,得标准方程;
(2)关键是把![]() 表示为一个变量的函数,当直线
表示为一个变量的函数,当直线![]() 斜率不存在时,可直接求出
斜率不存在时,可直接求出![]() 的长,当直线
的长,当直线![]() 斜率存在时,设其方程为
斜率存在时,设其方程为![]() ,与椭圆方程联立方程组,变形后由判别式写出一个不等关系,并设
,与椭圆方程联立方程组,变形后由判别式写出一个不等关系,并设![]() ,由韦达定理得出
,由韦达定理得出![]() ,由
,由![]() 表示出
表示出![]() 点坐标代入椭圆方程得
点坐标代入椭圆方程得![]() ,代入刚才的
,代入刚才的![]() 得
得![]() 的关系式:
的关系式:![]() ,它满足判别式>0,计算
,它满足判别式>0,计算![]() 中点
中点![]() 的坐标,再计算线段长
的坐标,再计算线段长![]() ,最终表示为
,最终表示为![]() 的函数,从而中求得取值范围.
的函数,从而中求得取值范围.
详解:(1)由题意,![]() ,
,![]() ,∴
,∴![]() ,
,
∴椭圆![]()
(2)设![]() ,
,![]() ,
,![]() ,
,
由![]()
∴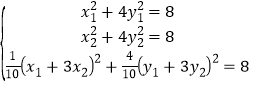 ,得:
,得:![]()
当![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,![]()
由![]() ,
,![]() ,得
,得![]() ,∴
,∴![]() ,
,![]()
当![]() 的斜率存在时,设
的斜率存在时,设![]()
![]() 得:
得:![]() ,
,![]()
![]() ,
,![]()
由![]() 点在椭圆上得
点在椭圆上得![]() 得:
得:![]() ,此时
,此时![]() 总成立
总成立
又![]() ,
,![]()
∴![]() ,
,![]()
∴![]() 且
且![]() ,∴
,∴![]() 且
且![]()
综上:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四种说法:
(1)函数
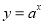
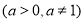 与函数
与函数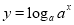
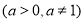 的定义域相同;
的定义域相同;(2)函数
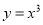 与
与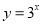 的值域相同;
的值域相同;(3)若函数
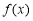 式定义在R上的偶函数且在
式定义在R上的偶函数且在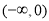 为减函数对于锐角
为减函数对于锐角 则
则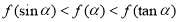 ;
;(4)若函数
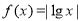 且
且
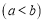 ,则
,则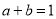 ;
;其中正确说法的序号是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱柱
 ,平面
,平面 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)证明:
 ;
;(2)求直线
 与平面
与平面 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
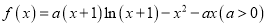 是减函数,则实数
是减函数,则实数 ( )
( )A.2B.1C.
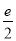 D.
D.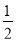
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=
 米,记∠BHE=
米,记∠BHE= .
.
(1)试将污水净化管道的长度L表示为
 的函数,并写出定义域;
的函数,并写出定义域;(2)当
 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数
 ,
, 是实数,
是实数, 是虚数单位.
是虚数单位.(1)求复数
 ;
;(2)若复数
 所表示的点在第一象限,求实数m的取值范围.
所表示的点在第一象限,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
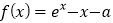 ,
,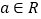 .
.(1)求函数
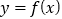 的单调区间及极值;
的单调区间及极值;(2)若
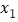 ,
,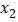 是函数
是函数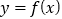 的两个不同零点,求证:①
的两个不同零点,求证:①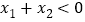 ;②
;②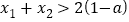 .
.
相关试题

