【题目】已知奇函数f(x),当x>0时f(x)=x+ ![]() ,则f(﹣1)=( )
,则f(﹣1)=( )
A.1
B.2
C.﹣1
D.﹣2
参考答案:
【答案】D
【解析】解:∵奇函数f(x)
∴f(﹣1)=﹣f(1)
而f(1)=1+1=2
∴f(﹣1)=﹣f(1)=﹣2
故选D
【考点精析】认真审题,首先需要了解函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇),还要掌握函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
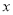 ,
, 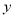 满足约束条件
满足约束条件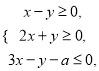 若目标函数
若目标函数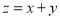 的最小值为
的最小值为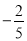 ,则实数
,则实数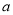 的值为
的值为A.
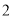 B.
B. 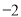 C.
C. 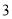 D.
D. 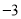
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=ln
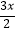 ﹣
﹣ 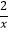 的零点一定位于区间( )
的零点一定位于区间( )
A.(1,2)
B.(2,3)
C.(3,4)
D.(4,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列表示错误的是( )
A.0??
B.??{1,2}
C.{(x,y)|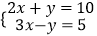 ={3,4}
={3,4}
D.若A?B,则A∩B=A -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两家快递公司其“快递小哥”的日工资方案如下:甲公司规定底薪
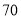 元,每单抽成
元,每单抽成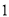 元;乙公司规定底薪
元;乙公司规定底薪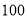 元,每日前
元,每日前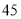 单无抽成,超过
单无抽成,超过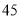 单的部分每单抽成
单的部分每单抽成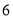 元
元(1)设甲乙快递公司的“快递小哥”一日工资
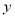 (单位:元)与送货单数
(单位:元)与送货单数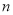 的函数关系式为
的函数关系式为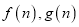 ,求
,求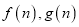 ;
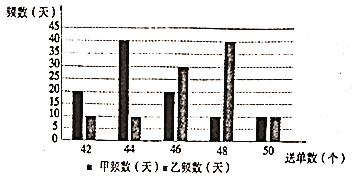
;(2)假设同一公司的“快递小哥”一日送货单数相同,现从两家公司各随机抽取一名“快递小哥”,并记录其
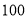 天的送货单数,得到如下条形图:
天的送货单数,得到如下条形图:若将频率视为概率,回答下列问题:
①记乙快递公司的“快递小哥”日工资为
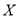 (单位:元),求
(单位:元),求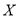 的分布列和数学期望;
的分布列和数学期望;②小赵拟到两家公司中的一家应聘“快递小哥”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的命题有__________.
①回归直线
 恒过样本点的中心
恒过样本点的中心 ,且至少过一个样本点;
,且至少过一个样本点;②将一组数据的每个数据都加一个相同的常数后,方差不变;
③用相关指数
 来刻画回归效果,
来刻画回归效果,  越接近
越接近 ,说明模型的拟合效果越好;
,说明模型的拟合效果越好;④用系统抽样法从
 名学生中抽取容量为
名学生中抽取容量为 的样本,将
的样本,将 名学生从
名学生从 编号,按编号顺序平均分成
编号,按编号顺序平均分成 组(
组( 号,
号,  号,
号,  号),若第
号),若第 组抽出的号码为
组抽出的号码为 ,则第一组中用抽签法确定的号码为
,则第一组中用抽签法确定的号码为 号.
号. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
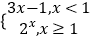 ,则满足f(f(a))=2f(a)的a的取值范围是( )
,则满足f(f(a))=2f(a)的a的取值范围是( )
A.[ ,1]
,1]
B.[0,1]
C.[ ,+∞)
,+∞)
D.[1,+∞)
相关试题

