【题目】在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,且
,且![]() 的面积
的面积![]() ,向量
,向量![]() .
.
(Ⅰ)求![]() 大小;
大小;
(Ⅱ)求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)利用三角形的面积公式化简已知等式的左边,利用余弦定理表示出![]() ,变形后代入等式的右边,利用同角三角函数间的基本关系弦化切整理后求出
,变形后代入等式的右边,利用同角三角函数间的基本关系弦化切整理后求出![]() 的值,由
的值,由![]() 为三角形的内角,利用特殊角的三角函数值即可求出
为三角形的内角,利用特殊角的三角函数值即可求出![]() 的度数;(Ⅱ)由
的度数;(Ⅱ)由![]() 的度数,利用三角形的内角和定理表示出
的度数,利用三角形的内角和定理表示出![]() 的度数,用
的度数,用![]() 表示出
表示出![]() ,代入所求的式子中,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,合并后再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据
,代入所求的式子中,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,合并后再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据![]() 的范围求出这个角的范围,利用正弦函数的图象与性质得出此时正弦函数的值域,即可得到所求式子的范围.
的范围求出这个角的范围,利用正弦函数的图象与性质得出此时正弦函数的值域,即可得到所求式子的范围.
试题解析:(Ⅰ)由余弦定理![]() ,则
,则![]() ,
,
另一方面![]() ,于是有
,于是有![]() ,即
,即![]()
解得![]() ,又
,又![]() ,故
,故![]() ;
;
(Ⅱ)![]() ,
, ![]()
![]()
![]()
∵![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,∴
,∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】运行如图所示的程序框图,则输出结果为( )
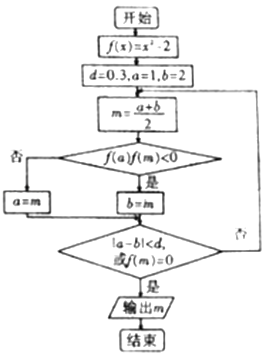
A.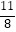
B.
C.
D.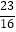
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
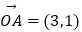 ,
, 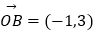 ,
, 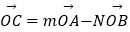 (m>0,n>0),若m+n∈[1,2],则
(m>0,n>0),若m+n∈[1,2],则 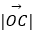 的取值范围是( )
的取值范围是( )
A.
B.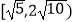
C.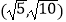
D.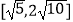
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=ex+mx2﹣m(m>0),当x1+x2=1时,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则实数x1的取值范围是( )
A.(﹣∞,0)
B.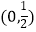
C.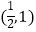
D.(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
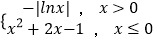 ,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
A.p假q真
B.p假q假
C.p真q真
D.p真q假 -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数h(x)=ax3+bx2+cx+d(a≠0)图象的对称中心为M(x0 , h(x0)),记函数h(x)的导函数为g(x),则有g′(x0)=0,设函数f(x)=x3﹣3x2+2,则f(
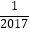 )+f(
)+f( 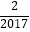 )+…+f(
)+…+f( 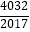 )+f(
)+f( 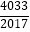 )= .
)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足
满足 ,且
,且 .
.(Ⅰ)证明:数列
 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;(Ⅱ)若记
 为满足不等式
为满足不等式 的正整数
的正整数 的个数,设
的个数,设 ,求数列
,求数列 的最大项与最小项的值.
的最大项与最小项的值.【答案】(1)见解析;(2)最大项为
 ,最小项为
,最小项为 .
.【解析】试题分析:(Ⅰ)对
 两边取倒数,移项即可得出
两边取倒数,移项即可得出 ,故而数列
,故而数列 为等差数列,利用等差数列的通项公式求出
为等差数列,利用等差数列的通项公式求出 ,从而可得出
,从而可得出 ;(Ⅱ)根据不等式
;(Ⅱ)根据不等式 ,,得
,,得 ,又
,又 ,从而
,从而 ,当
,当 为奇数时,
为奇数时, 单调递减,
单调递减, ;当
;当 为偶数时
为偶数时 单调递增,
单调递增, 综上
综上 的最大项为
的最大项为 ,最小项为
,最小项为 .
.试题解析:(Ⅰ)由于
 ,
, ,则
,则
∴
 ,则
,则 ,即
,即 为常数
为常数 又
 ,∴数列
,∴数列 是以1为首项,
是以1为首项, 为公比的等比数列
为公比的等比数列从而
 ,即
,即 .
.(Ⅱ)由
 即
即 ,得
,得 ,
,又
 ,从而
,从而
故

当
 为奇数时,
为奇数时, ,
, 单调递减,
单调递减, ;
;当
 为偶数时,
为偶数时, ,
, 单调递增,
单调递增,
综上
 的最大项为
的最大项为 ,最小项为
,最小项为 .
.【题型】解答题
【结束】
22【题目】已知向量
 ,
,
 ,若函数
,若函数 的最小正周期为
的最小正周期为 ,且在区间
,且在区间 上单调递减.
上单调递减.(Ⅰ)求
 的解析式;
的解析式;(Ⅱ)若关于
 的方程
的方程 在
在 有实数解,求
有实数解,求 的取值范围.
的取值范围.
相关试题

