【题目】已知{an}是递增的等差数列a3= ![]() ,且a2a4=6.
,且a2a4=6.
(1)求{an}的首项a1和公差d;
(2)求{an}的通项和前n项和Sn .
参考答案:
【答案】
(1)解:由题意得公差d>0,
a3= ![]() ,且a2a4=6,
,且a2a4=6,
可得a2+a4=2a3=5,
解得a2=2,a4=3,
可得2d=a4﹣a2=1,解得d= ![]() ,
,
则a1=a2﹣d= ![]() ;
;
(2)解:{an}的通项an=a1+(n﹣1)d= ![]() +
+ ![]() (n﹣1)=
(n﹣1)= ![]() (n+2);
(n+2);
前n项和Sn=na1+ ![]() n(n﹣1)d=
n(n﹣1)d= ![]() n+
n+ ![]() n(n﹣1)=
n(n﹣1)= ![]() n2+
n2+ ![]() n.
n.
【解析】(1)由题意得公差d>0,运用等差数列中项的性质,解方程可得a2=2,a4=3,运用等差数列的通项公式可得公差d和首项;(2)运用等差数列的通项公式和求和公式,化简计算即可得到所求.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系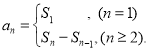 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线 过抛物线焦点,且与抛物线交于
过抛物线焦点,且与抛物线交于 ,
,  两点,以线段
两点,以线段 为直径的圆与抛物线准线的位置关系是( )
为直径的圆与抛物线准线的位置关系是( )A. 相离 B. 相交 C. 相切 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)将一颗骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,以分别得到的点数(m,n)作为点P的坐标(m,n),求:点P落在区域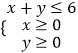 内的概率;
内的概率;
(2)在区间[1,6]上任取两个实数(m,n),求:使方程x2+mx+n2=0有实数根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 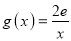 .
.(1)当
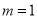 时,求
时,求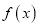 的单调区间;
的单调区间;(2)当
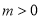 时,若存在
时,若存在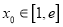 使得
使得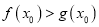 成立,求实数
成立,求实数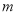 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的方程为x=﹣2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.
(1)过M点的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的 ,求直线l1的方程;
,求直线l1的方程;
(2)若椭圆中a,c满足 =2,求中心在原点,且与圆O恰有两个公共点的椭圆方程;
=2,求中心在原点,且与圆O恰有两个公共点的椭圆方程;
(3)过M点作直线l2与圆相切于点N,设(2)中椭圆的两个焦点分别为F1 , F2 , 求三角形△NF1F2面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
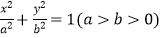 ,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线
,点A、B分别为其左、右顶点,点F1、F2分别为其左、右焦点,以点A为圆心,AF1为半径作圆A;以点B为圆心,OB为半径作圆B;若直线 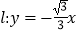 被圆A和圆B截得的弦长之比为
被圆A和圆B截得的弦长之比为 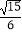 ;
; 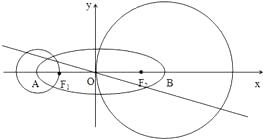
(1)求椭圆C的离心率;
(2)己知a=7,问是否存在点P,使得过P点有无数条直线被圆A和圆B截得的弦长之比为 ;若存在,请求出所有的P点坐标;若不存在,请说明理由.
;若存在,请求出所有的P点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“糖尿病”已经成为日渐多发的一种疾病,其具有危害性大且难以完全治愈的特征.为了更好的抑制“糖尿病”多发的势头,某社区卫生医疗机构针对所服务居民开展了免费测血糖活动,将随机抽取的10名居民均分为
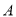 ,
, 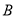 两组(
两组(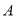 组:4.3,5.1,4.6,4.1,4.9;
组:4.3,5.1,4.6,4.1,4.9; 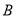 组:5.1,4.9,4.0,4.0,4.5).
组:5.1,4.9,4.0,4.0,4.5).(1)通过提供的数据请判断哪一组居民的血糖值更低;
(2)现从
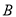 组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率.
组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率.
相关试题

