【题目】已知函数![]() 在
在![]() 时取得极小值.
时取得极小值.
(1)求实数![]() 的值;
的值;
(2)是否存在区间![]() ,使得
,使得![]() 在该区间上的值域为
在该区间上的值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由已知得![]() ,根据
,根据![]() 可得
可得![]() 或
或![]() .然后根据极值定义进行分别验证:当
.然后根据极值定义进行分别验证:当![]() 时,
时, ![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,符合题意;当
上为增函数,符合题意;当![]() 时,
时, ![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,不符合题意.(2)由区间定义知
上为减函数,不符合题意.(2)由区间定义知![]() ,因为
,因为![]() ,所以
,所以![]() .下面根据
.下面根据![]() 所在区间位置关系进行讨论:结合
所在区间位置关系进行讨论:结合![]() 得 ① 若
得 ① 若![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() .有唯一解为
.有唯一解为![]() .② 若
.② 若![]() ,则
,则![]() ,即
,即![]() 或
或![]() .根据对应函数单调性知不存在满足条件的
.根据对应函数单调性知不存在满足条件的![]() .
.
试题解析:(1)![]() ,
,
由题意知![]() ,解得
,解得![]() 或
或![]() . 2分
. 2分
当![]() 时,
时, ![]() ,
,
易知![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,符合题意;
上为增函数,符合题意;
当![]() 时,
时, ![]() ,
,
易知![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,不符合题意.
上为减函数,不符合题意.
所以,满足条件的![]() . 5分
. 5分
(2)因为![]() ,所以
,所以![]() . 7分
. 7分
① 若![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() . 9分
. 9分
设![]() ,则
,则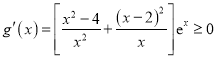 ,
,
所以![]() 在
在![]() 上为增函数.
上为增函数.
由于![]() ,即方程
,即方程![]() 有唯一解为
有唯一解为![]() . 11分
. 11分
② 若![]() ,则
,则![]() ,即
,即![]() 或
或![]() .
.
(Ⅰ)![]() 时,
时, 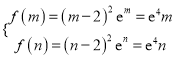 ,
,
由①可知不存在满足条件的![]() . 13分
. 13分
(Ⅱ)![]() 时,
时, 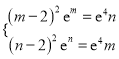 ,两式相除得
,两式相除得![]() .
.
设![]() ,
,
则![]() ,
,
![]() 在
在![]() 递增,在
递增,在![]() 递减,由
递减,由![]() 得
得![]() ,
, ![]() ,
,
此时![]() ,矛盾.
,矛盾.
综上所述,满足条件的![]() 值只有一组,且
值只有一组,且![]() . 16分
. 16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知f(x)=
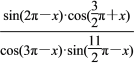 ,求f(-
,求f(-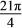 )的值
)的值(2)已知-π<x<0,sin(π+x)-cosx=-
 .
.①求sinx-cosx的值;②求
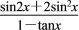 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
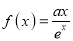 在
在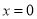 处的切线方程为
处的切线方程为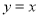 .
.(1)求
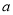 的值;(2)若对任意的
的值;(2)若对任意的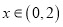 ,都有
,都有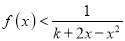 成立,求正数
成立,求正数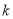 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若函数
 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;(2)若函数
 在
在 上的最小值为3,求实数
上的最小值为3,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数
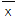 ≤3;②标准差S≤2;③平均数
≤3;②标准差S≤2;③平均数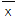 ≤3且标准差S≤2;④平均数
≤3且标准差S≤2;④平均数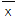 ≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.A.①② B.③④
C.③④⑤ D.④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a1|+|a2|+|a3|+|a4|+|a5|=32
②α,β,γ是三个不同的平面,则“γ⊥α,γ⊥β”是“α∥β”的充分条件
③已知sin
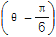 =
=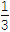 ,则cos
,则cos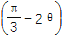 =
=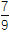 .其中正确命题的个数为( )
.其中正确命题的个数为( )A.0 B.1
C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在路边安装路灯,路宽为
 ,灯柱
,灯柱 长为
长为 米,灯杆
米,灯杆 长为1米,且灯杆与灯柱成
长为1米,且灯杆与灯柱成 角,路灯采用圆锥形灯罩,其轴截面的顶角为
角,路灯采用圆锥形灯罩,其轴截面的顶角为 ,灯罩轴线
,灯罩轴线 与灯杆
与灯杆 垂直.
垂直.⑴设灯罩轴线与路面的交点为
 ,若
,若 米,求灯柱
米,求灯柱 长;
长;⑵设
 米,若灯罩截面的两条母线所在直线一条恰好经过点
米,若灯罩截面的两条母线所在直线一条恰好经过点 ,另一条与地面的交点为
,另一条与地面的交点为 (如图2)
(如图2)

(图1) (图2)
(ⅰ)求
 的值;(ⅱ)求该路灯照在路面上的宽度
的值;(ⅱ)求该路灯照在路面上的宽度 的长.
的长.
相关试题

