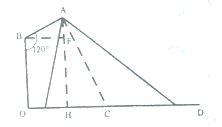
【题目】如图1,在路边安装路灯,路宽为![]() ,灯柱
,灯柱![]() 长为
长为![]() 米,灯杆
米,灯杆![]() 长为1米,且灯杆与灯柱成
长为1米,且灯杆与灯柱成![]() 角,路灯采用圆锥形灯罩,其轴截面的顶角为
角,路灯采用圆锥形灯罩,其轴截面的顶角为![]() ,灯罩轴线
,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直.
垂直.
⑴设灯罩轴线与路面的交点为![]() ,若
,若![]() 米,求灯柱
米,求灯柱![]() 长;
长;
⑵设![]() 米,若灯罩截面的两条母线所在直线一条恰好经过点
米,若灯罩截面的两条母线所在直线一条恰好经过点![]() ,另一条与地面的交点为
,另一条与地面的交点为![]() (如图2)
(如图2)


(图1) (图2)
(ⅰ)求![]() 的值;(ⅱ)求该路灯照在路面上的宽度
的值;(ⅱ)求该路灯照在路面上的宽度![]() 的长.
的长.
参考答案:
【答案】(1)灯柱![]() 长为13米.
长为13米.
(2)(ⅰ)![]() 值为
值为![]() ;(ⅱ)
;(ⅱ) ![]() 长为
长为![]() 米.
米.
【解析】试题分析:(1)在四边形OCAB内求解,先过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .再分别在直角三角形AHC,及ABF中求解
.再分别在直角三角形AHC,及ABF中求解![]() ,则
,则![]() (2)在
(2)在![]() 中,由余弦定理得
中,由余弦定理得![]() ,由正弦定理得
,由正弦定理得![]() ,即得
,即得![]() ;再由
;再由![]()
![]() 以及正弦定理得
以及正弦定理得![]()
试题解析:解:(1)过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
因为![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
解得![]() .
.
(2)(ⅰ)在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,所以
,所以![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,即
,即![]() ,
,
解得![]() ,所以
,所以![]() .
.
(ⅱ)![]() ,
, ![]() ,
,
所以![]()
![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,即
,即
![]()
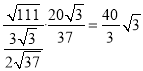 .
.
答:(1)灯柱![]() 长为13米.
长为13米.
(2)(ⅰ)![]() 值为
值为![]() ;(ⅱ)
;(ⅱ) ![]() 长为
长为![]() 米.
米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
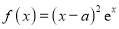 在
在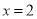 时取得极小值.
时取得极小值.(1)求实数
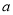 的值;
的值;(2)是否存在区间
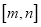 ,使得
,使得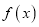 在该区间上的值域为
在该区间上的值域为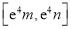 ?若存在,求出
?若存在,求出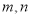 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数
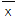 ≤3;②标准差S≤2;③平均数
≤3;②标准差S≤2;③平均数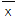 ≤3且标准差S≤2;④平均数
≤3且标准差S≤2;④平均数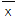 ≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.A.①② B.③④
C.③④⑤ D.④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a1|+|a2|+|a3|+|a4|+|a5|=32
②α,β,γ是三个不同的平面,则“γ⊥α,γ⊥β”是“α∥β”的充分条件
③已知sin
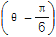 =
=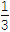 ,则cos
,则cos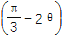 =
=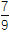 .其中正确命题的个数为( )
.其中正确命题的个数为( )A.0 B.1
C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数
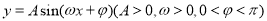 ,
,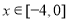 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.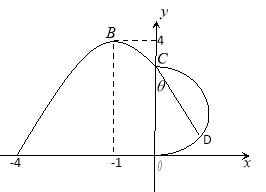
(1)试确定A,
 和
和 的值;
的值;(2)现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
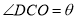 (弧度),试用
(弧度),试用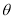 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度) -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式
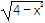 -kx+1≤0的解集非空,则k的取值范围为________.
-kx+1≤0的解集非空,则k的取值范围为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c.已知c=2,C=
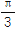 .
.(1)若△ABC的面积等于
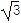 ,求a,b;
,求a,b;(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
相关试题

