【题目】在一个盒子里装有6张卡片,上面分别写着如下定义域为![]() 的函数:
的函数:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)现在从盒子中任意取两张卡片,记事件![]() 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件![]() 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为![]() ,写出
,写出![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]() .
.
参考答案:
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)根据函数的性质,两个奇函数的和是奇函数,而六个函数中有两个奇函数,根据排列组合知识 结合古典概型概率公式进行求解即可;(2)![]() 的所有可能取值为
的所有可能取值为![]() ,分别求概率, 列出分布列, 再求出期望即可.
,分别求概率, 列出分布列, 再求出期望即可.
试题解析:(1)由题意得![]() ,
,![]() 是奇函数,
是奇函数,![]() ,
,![]() ,
,![]() 为偶函数,
为偶函数,![]() 为非奇非偶函数,所以
为非奇非偶函数,所以![]() .
.
(2)由题意可知,![]() 的所有可能取值为1,2,3,4,
的所有可能取值为1,2,3,4,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 |
|
|
|
|
|
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知五边形
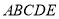 由直角梯形
由直角梯形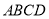 与直角△
与直角△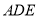 构成,如图1所示,
构成,如图1所示,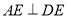 ,
,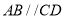 ,
,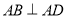 ,且
,且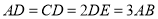 ,将梯形
,将梯形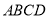 沿着
沿着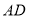 折起,形成如图2所示的几何体,且使平面
折起,形成如图2所示的几何体,且使平面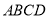
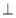 平面
平面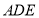 .
.
(1)在线段
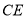 上存在点
上存在点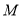 ,且
,且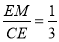 ,证明:
,证明: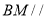 平面
平面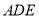 ;
;(2)求二面角
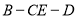 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
 的参数方程式
的参数方程式 (
( 是参数).以坐标原点为极点,
是参数).以坐标原点为极点, 轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.(1)求直线
 的普通方程与圆
的普通方程与圆 的直角坐标方程;
的直角坐标方程;(2)设圆
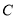 与直线
与直线 交于
交于 、
、 两点,若
两点,若 点的直角坐标为
点的直角坐标为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在简单随机抽样中,某一个个体被抽到的可能性( )
A.第一次被抽到的可能性最大B.第一次被抽到的可能性最小
C.每一次被抽到的可能性相等D.与抽取几个样本有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直三棱柱
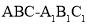 中,
中,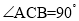 ,
, ,
, 是棱
是棱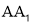 上的一点,
上的一点, 分别为
分别为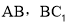 的中点.
的中点.
(1)求证:
 ∥平面
∥平面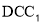 ;
;(2)当
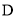 为
为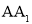 的中点时,求三棱锥
的中点时,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
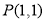 ,过点
,过点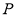 动直线
动直线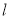 与圆
与圆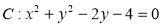 交与点
交与点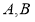 两点.
两点.(1)若
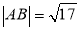 ,求直线
,求直线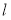 的倾斜角;
的倾斜角;(2)求线段
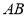 中点
中点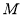 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期
4月1日
4月7日
4月15日
4月21日
4月30日
温差
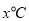
10
11
13
12
8
发芽数
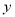 颗
颗23
25
30
26
16
(1)从这5天中任选2天,记发芽的种子数分别为
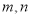 ,求事件“
,求事件“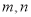 均不小于25”的概率;
均不小于25”的概率;(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出
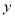 关于
关于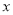 的线性回归方程
的线性回归方程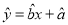 .
.(参考公式:
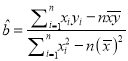 ,
, 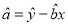 )
)
相关试题

