【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程式
的参数方程式 (
(![]() 是参数).以坐标原点为极点,
是参数).以坐标原点为极点,![]() 轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)将参数方程两式相加消去参数普通方程![]() 得到直线
得到直线![]() 的普通方程,将扱坐标方程展开两边同乘
的普通方程,将扱坐标方程展开两边同乘![]() ,根据极坐标与直角坐标的对应关系得到直角坐标方程;(2)将直线
,根据极坐标与直角坐标的对应关系得到直角坐标方程;(2)将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,利用根与系数的关系和参数的几何意义求出距离.
的直角坐标方程,利用根与系数的关系和参数的几何意义求出距离.
试题解析:(1)直线![]() 消去参数
消去参数![]() ,得
,得![]() ,
,
即直线![]() 的普通方程为
的普通方程为![]() .
.
由![]() ,得
,得![]() ,
,
∴![]() ,
,
∴圆![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)点![]() 在直线
在直线![]() 上,且在圆
上,且在圆![]() 内,
内,
把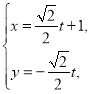 代入
代入![]() ,
,
得![]() ,
,
设两个实根为![]() ,
,![]() ,则
,则![]() 、
、![]() 两点所对应的参数为
两点所对应的参数为![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∴![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
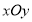 中,以原点
中,以原点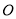 为极点,以
为极点,以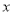 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线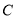 的极坐标方程为
的极坐标方程为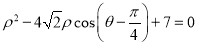 .
.(1)求曲线
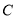 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;(2)设
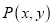 是曲线
是曲线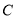 上的动点,求
上的动点,求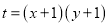 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知五边形
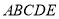 由直角梯形
由直角梯形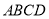 与直角△
与直角△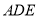 构成,如图1所示,
构成,如图1所示,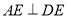 ,
,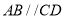 ,
,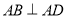 ,且
,且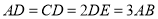 ,将梯形
,将梯形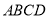 沿着
沿着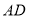 折起,形成如图2所示的几何体,且使平面
折起,形成如图2所示的几何体,且使平面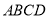
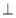 平面
平面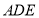 .
.
(1)在线段
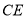 上存在点
上存在点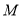 ,且
,且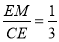 ,证明:
,证明: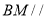 平面
平面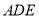 ;
;(2)求二面角
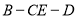 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在简单随机抽样中,某一个个体被抽到的可能性( )
A.第一次被抽到的可能性最大B.第一次被抽到的可能性最小
C.每一次被抽到的可能性相等D.与抽取几个样本有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个盒子里装有6张卡片,上面分别写着如下定义域为
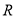 的函数:
的函数: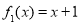 ,
,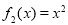 ,
,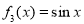 ,
,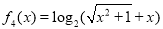 ,
,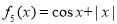 ,
,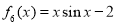 .
.(1)现在从盒子中任意取两张卡片,记事件
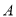 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件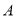 的概率;
的概率;(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为
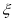 ,写出
,写出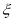 的分布列,并求其数学期望
的分布列,并求其数学期望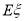 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直三棱柱
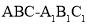 中,
中,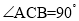 ,
, ,
,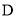 是棱
是棱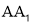 上的一点,
上的一点, 分别为
分别为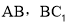 的中点.
的中点.
(1)求证:
 ∥平面
∥平面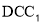 ;
;(2)当
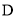 为
为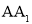 的中点时,求三棱锥
的中点时,求三棱锥 的体积.
的体积.
相关试题

