【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)如果对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,若存在,求出
的最大值为0,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
参考答案:
【答案】(1)[0,2];(2)(-∞,![]() );(3)答案见解析.
);(3)答案见解析.
【解析】试题分析:(1)由h(x)=-2(log3x-1)2+2,根据log3x∈[0,2],即可得值域;
(2)由![]() ,令t=log3x,因为x∈[1,9],所以t=log3x∈[0,2],得(3-4t)(3-t)>k对一切t∈[0,2]恒成立,利用二次函数求函数的最小值即可;
,令t=log3x,因为x∈[1,9],所以t=log3x∈[0,2],得(3-4t)(3-t)>k对一切t∈[0,2]恒成立,利用二次函数求函数的最小值即可;
(3)由![]() ,假设最大值为0,因为
,假设最大值为0,因为![]() ,则有
,则有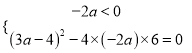 ,求解即可.
,求解即可.
试题解析:
(1)h(x)=(4-2log3x)·log3x=-2(log3x-1)2+2,
因为x∈[1,9],所以log3x∈[0,2],
故函数h(x)的值域为[0,2].
(2)由![]() ,
,
得(3-4log3x)(3-log3x)>k,
令t=log3x,因为x∈[1,9],所以t=log3x∈[0,2],
所以(3-4t)(3-t)>k对一切t∈[0,2]恒成立,
令![]() ,其对称轴为
,其对称轴为![]() ,
,
所以当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,
,
综上,实数k的取值范围为(-∞,![]() )..
)..
(3)假设存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,
的最大值为0,
由![]() .
.
因为![]() ,则有
,则有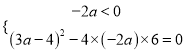 ,解得
,解得![]() ,所以不存在实数
,所以不存在实数![]() ,
,
使得函数![]() 的最大值为0.
的最大值为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在
是定义在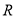 上的奇函数,当
上的奇函数,当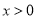 时,
时, 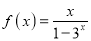 .
.(1)求
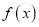 的解析式;
的解析式;(2)解不等式
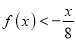 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
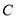 经过点
经过点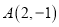 ,
,  和直线
和直线 相切.
相切.(1)求圆
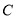 的方程;
的方程;(2)若直线
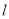 经过点
经过点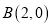 ,并且被圆
,并且被圆 截得的弦长为2,求直线
截得的弦长为2,求直线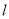 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四面体
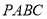 中,
中, 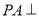 平面
平面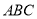 ,
, 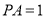 ,
, 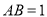 ,
,  ,
,  .
.(Ⅰ)求四面体
 的四个面的面积中,最大的面积是多少?
的四个面的面积中,最大的面积是多少?(Ⅱ)证明:在线段
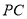 上存在点
上存在点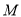 ,使得
,使得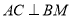 ,并求
,并求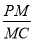 的值.
的值.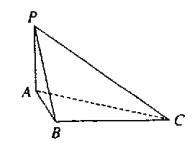
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
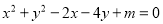 .
.(Ⅰ)若此方程表示圆,求
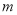 的取值范围;
的取值范围;(Ⅱ)若(Ⅰ)中的圆与直线
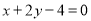 相交于
相交于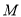 ,
, 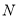 两点,且
两点,且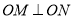 (
(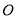 为坐标原点),求
为坐标原点),求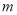 ;
;(Ⅲ)在(Ⅱ)的条件下,求以
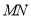 为直径的圆的方程.
为直径的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=
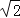 ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.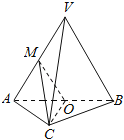
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别是棱长为1的正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是 .
相关试题

