【题目】已知![]() ,设函数
,设函数![]() .
. ![]()
(1)当![]() 时,求
时,求![]() 的极值点;
的极值点;
(2)讨论![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(3)![]() 对任意
对任意![]() 恒成立时,
恒成立时, ![]() 的最大值为1,求
的最大值为1,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 是
是![]() 的极小值点,无极大值点;(2)见解析;(3)
的极小值点,无极大值点;(2)见解析;(3)![]() .
.
【解析】【试题分析】(1)先求导数,再解方程求导函数的零点;(2)运用导数与函数的单调性之间的关系分析探求;(3)先将不等式进行等价转化,再分离参数,构造函数运用导数知识求解:
(1)当![]() 时,
时, ![]() ,∴
,∴![]() ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,所以
,所以![]() 是
是![]() 的极小值点,无极大值点.
的极小值点,无极大值点.
(2)![]() ,
,
①当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上单调递增;在
上单调递增;在![]() 上单调递减,
上单调递减,
②当![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
③当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
④当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(3)∵![]() ,
, ![]() 。由
。由![]() 得
得
![]() 对任意
对任意![]() 恒成立,即
恒成立,即
![]()
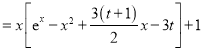 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,
, ![]() ,根据题意,可以知道
,根据题意,可以知道![]() 的最大值为1,则
的最大值为1,则![]()
![]()
![]() 恒成立.
恒成立.
由于![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
从而![]() ,满足条件,故
,满足条件,故![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定点
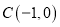 及椭圆
及椭圆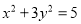 ,过点
,过点 的动直线与椭圆相交于
的动直线与椭圆相交于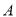 ,
,  两点.
两点.(1)若线段
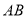 中点的横坐标是
中点的横坐标是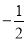 ,求直线
,求直线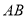 的方程;
的方程;(2)设点
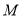 的坐标为
的坐标为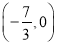 ,求证:
,求证: 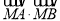 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)
已知椭圆
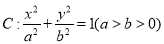 的短轴长为
的短轴长为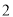 ,且与抛物线
,且与抛物线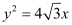 有共同的焦点,椭圆
有共同的焦点,椭圆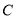 的左顶点为A,右顶点为
的左顶点为A,右顶点为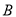 ,点
,点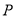 是椭圆
是椭圆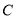 上位于
上位于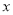 轴上方的动点,直线
轴上方的动点,直线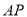 ,
,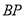 与直线
与直线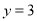 分别交于
分别交于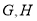 两点.
两点.(I)求椭圆
 的方程;
的方程;(Ⅱ)求线段
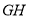 的长度的最小值;
的长度的最小值;(Ⅲ)在线段
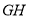 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆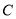 上是否存在一点
上是否存在一点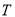 ,使得
,使得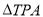 的面积为
的面积为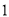 ,若存在求出点
,若存在求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1,
 ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;(1)求证:BD⊥平面
 ;
;(2)若
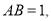 且
且 ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
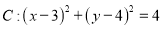 和直线
和直线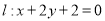 ,直线
,直线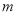 ,
, 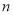 都经过圆
都经过圆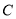 外定点
外定点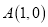 .
.(1)若直线
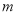 与圆
与圆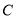 相切,求直线
相切,求直线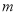 的方程;
的方程;(2)若直线
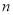 与圆
与圆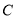 相交于
相交于 两点,与
两点,与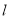 交于
交于 点,且线段
点,且线段 的中点为
的中点为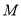 ,
,求证:
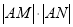 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
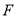 是拋物线
是拋物线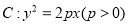 的焦点, 若点
的焦点, 若点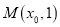 在
在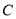 上,且
上,且 .
.(1)求
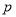 的值;
的值;(2)若直线
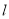 经过点
经过点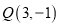 且与
且与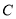 交于
交于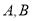 (异于
(异于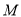 )两点, 证明: 直线
)两点, 证明: 直线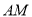 与直线
与直线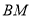 的斜率之积为常数.
的斜率之积为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系内三点
 .
.(1) 求过
 三点的圆的方程,并指出圆心坐标与圆的半径;
三点的圆的方程,并指出圆心坐标与圆的半径;(2)求过点
 与条件 (1) 的圆相切的直线方程.
与条件 (1) 的圆相切的直线方程.
相关试题

