【题目】已知定点![]() 及椭圆
及椭圆![]() ,过点
,过点![]() 的动直线与椭圆相交于
的动直线与椭圆相交于![]() ,
, ![]() 两点.
两点.
(1)若线段![]() 中点的横坐标是
中点的横坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设点![]() 的坐标为
的坐标为![]() ,求证:
,求证: ![]() 为定值.
为定值.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】试题分析:(1)将直线的点斜式方程(其中斜率为参数)代入椭圆方程,并设出交点A,B的坐标,消去Y后,可得一个关于X的一元二次方程,然后根据韦达定理(一元二次方程根与系数关系)易得A、B两点中点的坐标表达式,再由AB中点的横坐标是![]() ,,构造方程,即可求出直线的斜率,进而得到直线的方程.(2)由M点的坐标,我们易给出两个向量的坐标,然后代入平面向量数量集公式,结合韦达定理(一元二次方程根与系数关系),不难不求出
,,构造方程,即可求出直线的斜率,进而得到直线的方程.(2)由M点的坐标,我们易给出两个向量的坐标,然后代入平面向量数量集公式,结合韦达定理(一元二次方程根与系数关系),不难不求出![]() 的值.
的值.
试题解析:
(Ⅰ)依题意,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
将![]() 代入
代入![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
![]() .
.
设![]() ,
, ![]() ,
,
则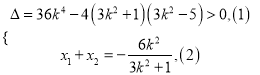 ,
,
由线段![]() 中点的横坐标是
中点的横坐标是![]() ,
,
得![]() ,
,
解得![]() ,适合(
,适合(![]() ).
).
所以直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.
(Ⅱ)①当直线![]() 与
与![]() 轴不垂直时,
轴不垂直时,
由(I)知![]() ,
, ![]() .(
.(![]() ),
),
所以![]() ,
,
![]() .
.
将(![]() )代入,整理得:
)代入,整理得:
 ,
,
![]() .
.
②当直线![]() 与
与![]() 轴垂直时,
轴垂直时,
此时点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
此时亦有![]() .
.
综上, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=x3+2x2﹣4x+5在[﹣4,1]上的最大值和最小值分别是( )
A.13,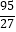
B.4,﹣11
C.13,﹣11
D.13,最小值不确定 -
科目: 来源: 题型:
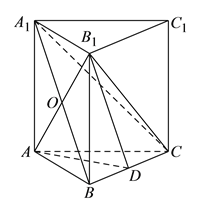
查看答案和解析>>【题目】如图,在直三棱柱
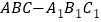 中,
中, ,
,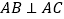 ,
,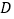 为
为 中点,
中点,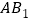 与
与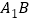 交于点
交于点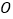 .
.
(1)求证:
 平面
平面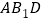 ;
;(2)求证:
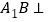 平面
平面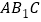 ;
;(3)求三棱锥
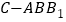 的表面积.
的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
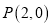 ,⊙
,⊙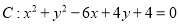 .
.(Ⅰ)当直线
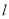 过点
过点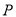 且与圆心
且与圆心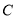 的距离为
的距离为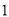 时,求直线
时,求直线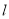 的方程.
的方程.(Ⅱ)设过点
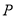 的直线与⊙
的直线与⊙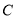 交于
交于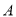 ,
, 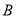 两点,且
两点,且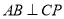 ,求以线段
,求以线段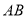 为直径的圆的方程.
为直径的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)
已知椭圆
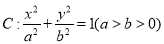 的短轴长为
的短轴长为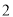 ,且与抛物线
,且与抛物线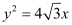 有共同的焦点,椭圆
有共同的焦点,椭圆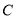 的左顶点为A,右顶点为
的左顶点为A,右顶点为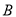 ,点
,点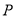 是椭圆
是椭圆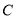 上位于
上位于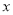 轴上方的动点,直线
轴上方的动点,直线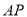 ,
,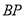 与直线
与直线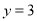 分别交于
分别交于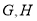 两点.
两点.(I)求椭圆
 的方程;
的方程;(Ⅱ)求线段
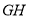 的长度的最小值;
的长度的最小值;(Ⅲ)在线段
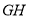 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆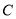 上是否存在一点
上是否存在一点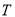 ,使得
,使得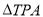 的面积为
的面积为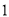 ,若存在求出点
,若存在求出点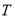 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1,
 ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;(1)求证:BD⊥平面
 ;
;(2)若
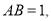 且
且 ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
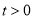 ,设函数
,设函数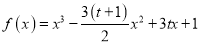 .
. 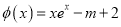
(1)当
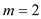 时,求
时,求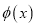 的极值点;
的极值点;(2)讨论
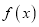 在区间
在区间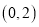 上的单调性;
上的单调性;(3)
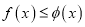 对任意
对任意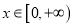 恒成立时,
恒成立时, 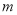 的最大值为1,求
的最大值为1,求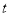 的取值范围.
的取值范围.
相关试题

