【题目】已知点![]() 是拋物线
是拋物线![]() 的焦点, 若点
的焦点, 若点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求![]() 的值;
的值;
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 交于
交于![]() (异于
(异于![]() )两点, 证明: 直线
)两点, 证明: 直线![]() 与直线
与直线![]() 的斜率之积为常数.
的斜率之积为常数.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)根据抛物线焦半径公式及点![]() 在
在![]() 上列方程组可求得
上列方程组可求得![]() 的值;(2)设
的值;(2)设![]() ,
, ![]()
![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程![]() ,消
,消![]() 得,
得, ![]() ,根据韦达定理可得
,根据韦达定理可得![]() .
.
试题解析:(1)由抛物线定义知![]() ,则
,则![]() ,解得
,解得![]() ,又点
,又点![]() 在
在![]() 上, 代入
上, 代入![]() ,得
,得![]() ,解得
,解得![]() .
.
(2)由(1)得![]() ,当直线
,当直线![]() 经过点
经过点![]() 且垂直于
且垂直于![]() 轴时, 此时
轴时, 此时![]() ,
,
则直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,所以
,所以![]() .当直线
.当直线![]() 不垂直于
不垂直于![]() 轴时, 设
轴时, 设![]() ,
,
则直线![]() 的斜率
的斜率![]() ,同理直线
,同理直线![]() 的斜率
的斜率![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,且经过
,且经过![]() ,则 直线
,则 直线![]() 的方程为
的方程为![]() .联立方程
.联立方程![]() ,消
,消![]() 得,
得, ![]() ,
,
所以![]() ,故
,故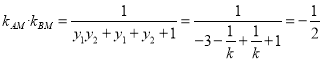 ,
,
综上, 直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1,
 ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;(1)求证:BD⊥平面
 ;
;(2)若
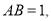 且
且 ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
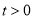 ,设函数
,设函数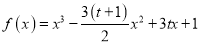 .
. 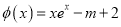
(1)当
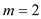 时,求
时,求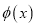 的极值点;
的极值点;(2)讨论
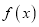 在区间
在区间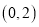 上的单调性;
上的单调性;(3)
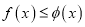 对任意
对任意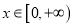 恒成立时,
恒成立时, 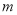 的最大值为1,求
的最大值为1,求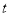 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
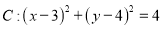 和直线
和直线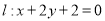 ,直线
,直线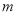 ,
, 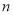 都经过圆
都经过圆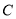 外定点
外定点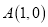 .
.(1)若直线
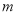 与圆
与圆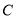 相切,求直线
相切,求直线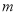 的方程;
的方程;(2)若直线
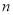 与圆
与圆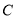 相交于
相交于 两点,与
两点,与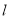 交于
交于 点,且线段
点,且线段 的中点为
的中点为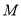 ,
,求证:
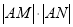 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系内三点
 .
.(1) 求过
 三点的圆的方程,并指出圆心坐标与圆的半径;
三点的圆的方程,并指出圆心坐标与圆的半径;(2)求过点
 与条件 (1) 的圆相切的直线方程.
与条件 (1) 的圆相切的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
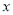 的方程
的方程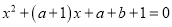 的两个根分别为
的两个根分别为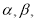 其中
其中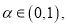
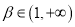 ,则
,则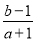 的取值范围是( )
的取值范围是( )A.
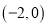 B.
B. 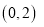 C.
C. 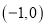 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入
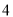 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从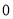 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.](1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入
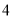 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入
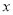 (单位:万元)
(单位:万元)1
2
3
4
5
销售收益
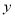 (单位:万元)
(单位:万元)2
3
2
7
由表中的数据显示,
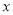 与
与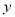 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出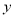 关于
关于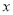 的回归直线方程.
的回归直线方程.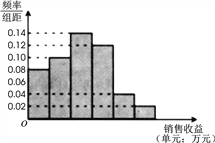
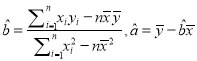
相关试题

