【题目】已知正数数列{an}的前n项和为Sn , 点P(an , Sn)在函数f(x)= ![]() x2+
x2+ ![]() x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
(1)求数列{an}的通项公式;
(2)若cn=anbn , 求数列{cn}的前n项和Tn;
(3)是否存在整数m,M,使得m<Tn<M对任意正整数n恒成立,且M﹣m=9,说明理由.
参考答案:
【答案】
(1)解:∵点P(an,Sn)在函数f(x)= ![]() x2+
x2+ ![]() x上,
x上,
∴Sn= ![]()
![]() +
+ ![]() an,Sn﹣1=
an,Sn﹣1= ![]()
![]() +
+ ![]() an﹣1(n≥2),
an﹣1(n≥2),
两式相减,整理得:(an+an﹣1)(an﹣an﹣1﹣1)=0,
又∵an>0,
∴an=an﹣1+1,
又∵S1= ![]()
![]() +
+ ![]() a1,即a1=1,
a1,即a1=1,
∴数列{an}是首项和公差均为1的等差数列,
∴an=n;
(2)解:∵b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
∴数列{bn}是首项为1、公比为 ![]() 的等比数列,
的等比数列,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
![]() Tn=
Tn= ![]() +2×
+2× ![]() +…+n×
+…+n× ![]() ,
,
两式相减,得: ![]() Tn=1+
Tn=1+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣n×
﹣n× ![]()
= ![]() ﹣n×
﹣n× ![]()
=3﹣(n+3)× ![]() ,
,
∴Tn=9﹣(3n+9)× ![]()
(3)解:结论:假设存在整数m、M,使得m<Tn<M对任意正整数n恒成立,且M﹣m=9.
理由如下:
由(2)知:Tn=9﹣(3n+9)× ![]() <9,
<9,
又∵Tn﹣1=9﹣[3(n﹣1)+9]× ![]() ,
,
∴Tn﹣Tn﹣1=(3n+6)× ![]() ﹣(3n+9)×
﹣(3n+9)× ![]() =n×
=n× ![]() >0,
>0,
∴数列{Tn}是单调递增数列,
∴(Tn)min=T1=9﹣12× ![]() =1,
=1,
∴1<Tn<9,
∴m=0,M=9,
∴存在整数m、M,使得m<Tn<M对任意正整数n恒成立,且M﹣m=9.
【解析】(1)通过将点P(an , Sn)代入函数f(x)= ![]() x2+
x2+ ![]() x中,利用Sn=
x中,利用Sn= ![]()
![]() +
+ ![]() an与Sn﹣1=
an与Sn﹣1= ![]()
![]() +
+ ![]() an﹣1(n≥2)作差,进而可知数列{an}是首项和公差均为1的等差数列,计算即得结论;(2)利用错位相减法计算即得结论;(3)通过(2)知Tn<9,利用作差法可知数列{Tn}是单调递增数列,进而计算可得结论.
an﹣1(n≥2)作差,进而可知数列{an}是首项和公差均为1的等差数列,计算即得结论;(2)利用错位相减法计算即得结论;(3)通过(2)知Tn<9,利用作差法可知数列{Tn}是单调递增数列,进而计算可得结论.
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系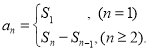 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为
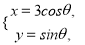 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为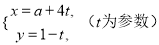 .
.(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为
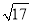 ,求a.
,求a. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,B1C和平面ABCD所成的角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( )
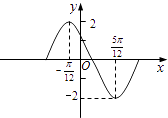
A.y=2sin(2x+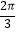 )
)
B.y=2sin(2x+ )
)
C.y=2sin( ﹣
﹣  )
)
D.y=2sin(2x﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】记Sn为等比数列
 的前n项和,已知S2=2,S3=-6.
的前n项和,已知S2=2,S3=-6.(1)求
 的通项公式;
的通项公式;(2)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列。
相关试题

