【题目】已知圆C的方程:x2+y2﹣4x﹣6y+m=0,若圆C与直线a:x+2y﹣3=0相交于M、N两点,且|MN|=2 ![]() .
.
(1)求m的值;
(2)是否存在直线l:x﹣y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围;若不存在,请说明理由.
,若存在,求出c的范围;若不存在,请说明理由.
参考答案:
【答案】
(1)解:方程x2+y2﹣4x﹣6y+m=0配方为(x﹣2)2+(y﹣3)2=13﹣m.
∵此方程表示圆,
∴13﹣m>0,即m<13.r= ![]() ,
,
圆C与直线a:x+2y﹣3=0相交于M、N两点,且|MN|=2 ![]() .
.
圆的圆心到直线的距离为:d= ![]() =
= ![]() .
.
可得 ![]() .
.
即:5=13﹣m﹣3,解得m=5
(2)解:(x﹣2)2+(y﹣3)2=8.圆的圆心(2,3),半径为2 ![]()
直线l:x﹣y+c=0,使得圆上有四点到直线l的距离为 ![]() ,
,
则圆心C(2,3)到直线l:x﹣y+c=0的距离为: ![]() =
= ![]() ,
,
可得:2 ![]() ﹣
﹣ ![]() >
> ![]() ,
,
解得﹣2<c<4
【解析】(1)由方程x2+y2﹣4x﹣6y+m=0配方为(x﹣2)2+(y﹣3)2=13﹣m.由于此方程表示圆,可得13﹣m>0,解出m的范围,利用弦心距与半径半弦长的关系,求解m即可.(2)求出圆心与半径,利用半径与圆的圆心到直线的距离的差大于 ![]() ,列出不等式求解即可.
,列出不等式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 为圆
为圆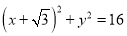 ,
, 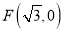 ,
, 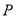 是圆上的动点,线段
是圆上的动点,线段 的垂直平分线交
的垂直平分线交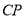 于点
于点 .
.(1)求点
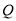 的轨迹
的轨迹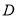 的方程;
的方程;(2)设
 ,
, 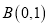 ,过点
,过点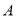 的直线
的直线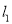 与曲线
与曲线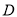 交于点
交于点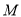 (异于点
(异于点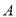 ),过点
),过点 的直线
的直线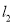 与曲线
与曲线 交于点
交于点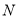 ,直线
,直线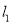 与
与 倾斜角互补.
倾斜角互补.①直线
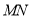 的斜率是否为定值?若是,求出该定值;若不是,说明理由;
的斜率是否为定值?若是,求出该定值;若不是,说明理由;②设
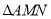 与
与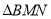 的面积之和为
的面积之和为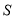 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,向量
,向量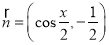 ,函数
,函数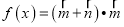 .
.(1)求
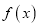 的单调减区间;
的单调减区间;(2)将函数
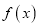 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移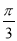 个单位长度,得到
个单位长度,得到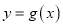 的图象,求函数
的图象,求函数 的解析式及其图象的对称中心.
的解析式及其图象的对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的三个顶点
的三个顶点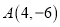 ,
, 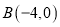 ,
,  ,求:
,求:(1)
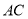 边上的高
边上的高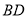 所在直线的方程;
所在直线的方程;(2)
 的垂直平分线
的垂直平分线 所在直线的方程;
所在直线的方程;(3)
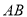 边的中线的方程.
边的中线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
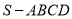 中,平面
中,平面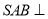 平面
平面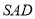 ,侧面
,侧面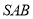 是边长为
是边长为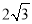 的等边三角形,底面
的等边三角形,底面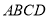 是矩形,且
是矩形,且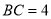 ,则该四棱锥外接球的表面积等于__________.
,则该四棱锥外接球的表面积等于__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如下表:
学生编号
1
2
3
4
5
6
语文成绩

60
70
74
90
94
110
历史成绩
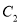
58
63
75
79
81
88
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩
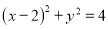 与语文成绩
与语文成绩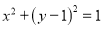 具有较强的线性相关关系,求
具有较强的线性相关关系,求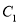 与
与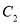 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).参考公式:回归直线方程是
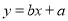 ,其中
,其中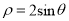 ,
, 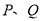
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下2×2的列联表:
喜欢该项运动
不喜欢该项运动
总计
男
40
20
60
女
20
30
50
总计
60
50
110
由公式
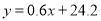 ,算得
,算得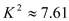
附表:
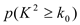
0.025
0.01
0.005
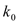
5.024
6.635
7.879
参照附表,以下结论正确是( )
A. 有
 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”B. 有
 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”C. 有
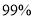 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”D. 有
 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
相关试题

