【题目】设a为实常数,y=f(x)是定义在R上的奇函数,当x<0时,f(x)=9x+ ![]() +7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
+7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
参考答案:
【答案】![]()
【解析】解:因为y=f(x)是定义在R上的奇函数,
所以当x=0时,f(x)=0;
当x>0时,则﹣x<0,所以f(﹣x)=﹣9x﹣ ![]() +7
+7
因为y=f(x)是定义在R上的奇函数,
所以f(x)=9x+ ![]() ﹣7;
﹣7;
因为f(x)≥a+1对一切x≥0成立,
所以当x=0时,0≥a+1成立,
所以a≤﹣1;
当x>0时,9x+ ![]() ﹣7≥a+1成立,
﹣7≥a+1成立,
只需要9x+ ![]() ﹣7的最小值≥a+1,
﹣7的最小值≥a+1,
因为9x+ ![]() ﹣7≥2
﹣7≥2 ![]() =6|a|﹣7,
=6|a|﹣7,
所以6|a|﹣7≥a+1,
解得 ![]() ,
,
所以 ![]() .
.
故答案为: ![]() .
.
先利用y=f(x)是定义在R上的奇函数求出x≥0时函数的解析式,将f(x)≥a+1对一切x≥0成立转化为函数的最小值≥a+1,利用基本不等式求出f(x)的最小值,解不等式求出a的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 是两个单位向量,与
是两个单位向量,与 ,
, 共面的向量
共面的向量 满足
满足 ,则
,则 的最大值为( )
的最大值为( )A.
 B. 2C.
B. 2C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,内角
,内角 的平分线
的平分线 的长为7,且
的长为7,且 ,则
,则 _____;
_____; 的长是______.
的长是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015秋随州期末)甲命题:若随机变量ξ~N(3,σ2),若P(ξ≤2)=0.3,则P(ξ≤4)=0.7.乙命题:随机变量η﹣B(n,p),且Eη=300,Dη=200,则P=
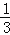 ,则正确的是( )
,则正确的是( )A. 甲正确乙错误 B. 甲错误乙正确
C. 甲错误乙也错误 D. 甲正确乙也正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(Ⅰ)当
 时,解不等式:
时,解不等式: ;
;(Ⅱ)当
 时,
时, 存在最小值
存在最小值 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
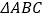 中,内角
中,内角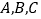 所对的边分别为
所对的边分别为 ,已知
,已知 .
.(Ⅰ)求角
 的值;
的值;(Ⅱ)记
 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段
 的长度为a,在线段
的长度为a,在线段 上取两个点
上取两个点 ,
, ,使得
,使得 ,以
,以 为一边在线段
为一边在线段 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段 ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
记第
 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为 ,现给出有关数列
,现给出有关数列 的四个命题:
的四个命题:①数列
 是等比数列;
是等比数列;②数列
 是递增数列;
是递增数列;③存在最小的正数
 ,使得对任意的正整数
,使得对任意的正整数 ,都有
,都有 ;
;④存在最大的正数
 ,使得对任意的正整数
,使得对任意的正整数 ,都有
,都有 .
.其中真命题的序号是________________(请写出所有真命题的序号).
相关试题

