【题目】解答题
(1)从0,1,2,3,4,5这六个数字任取3个,问能组成多少个没有重复数字的三位数?
(2)若(x6+3)(x2+ ![]() )5的展开式中含x10项的系数为43,求实数a的值.
)5的展开式中含x10项的系数为43,求实数a的值.
参考答案:
【答案】
(1)解:从0,1,2,3,4,5这六个数字任取3个,
能组成没有重复数字的三位数的个数是
![]()
![]() =5×5×4=100
=5×5×4=100
(2)解:(x6+3)(x2+ ![]() )5=x6
)5=x6 ![]() +3
+3 ![]() ,
,
且二项式 ![]() 展开式的通项公式为
展开式的通项公式为
Tr+1= ![]() x2(5﹣r)
x2(5﹣r) ![]() =
= ![]() x10﹣3rar;
x10﹣3rar;
令10﹣3r=10,解得r=0,
∴其展开式中x10的系数为 ![]() a0=1;
a0=1;
令10﹣3r=4,解得r=2,
∴其展开式中x4的系数为 ![]() a2=10a2;
a2=10a2;
故所求展开式中含x10项的系数为
10a2+3×1=43,
解得a=±2
【解析】(1)可用分步原理求解,第一步排首位,从非零数字中选一个,有 ![]() 种不同方法;第二步排后两位,从余下的5个数字中选2个排列即可;(2)化(x6+3)(x2+
种不同方法;第二步排后两位,从余下的5个数字中选2个排列即可;(2)化(x6+3)(x2+ ![]() )5=x6
)5=x6 ![]() +3
+3 ![]() , 利用
, 利用 ![]() 展开式的通项公式求出x10的系数和x4的系数,
展开式的通项公式求出x10的系数和x4的系数,
即可得出所求展开式中含x10项的系数,列方程求出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣
 <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ 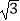 ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 
(1)求函数f(x)的解析式;
(2)若方程3[f(x)]2﹣f(x)+m=0在x∈( ,
,  )内有两个不同的解,求实数m的取值范围.
)内有两个不同的解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=Asin(ωx+φ)(其中A>0,
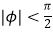 )的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( ) 
A.向右平移 个长度单位
个长度单位
B.向右平移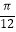 个长度单位
个长度单位
C.向左平移 个长度单位
个长度单位
D.向左平移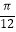 个长度单位
个长度单位 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列3个命题: 1)函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
3)y=x2﹣2|x|﹣3的递增区间为[1,+∞).
其中正确命题的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 x3﹣x2+x.
x3﹣x2+x.
(1)求函数f(x)在[﹣1,2]上的最大值和最小值;
(2)若函数g(x)=f(x)﹣4x,x∈[﹣3,2],求g(x)的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A、B、C所对的边分别为a,b,c且a=5,sinA=
 .
.
(I)若S△ABC= ,求周长l的最小值;
,求周长l的最小值;
(Ⅱ)若cosB= ,求边c的值.
,求边c的值.
相关试题

