【题目】如图,已知平面![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是菱形,且
是菱形,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点.
上的动点.
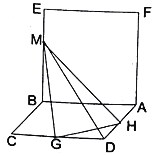
(1)求证:![]()
![]() ;
;
(2)求三棱锥![]() 的体积的最大值.
的体积的最大值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】【试题分析】(1)依据题设条件,运用线面垂直的性质定理推证;(2)借助题设条件,运用三棱锥的体积公式建立目标函数,通过探求函数的变量之间的联系分析探求最大值:
(1)证明:连接![]() 、
、![]() 相交于点
相交于点![]() .
.
因为四边形![]() 为正方形,所以
为正方形,所以![]() ,
,
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,所以
,所以![]() .
.
因为四边形![]() 为菱形,所以
为菱形,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() ,则
,则![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解:在菱形![]() 中,由
中,由![]() ,得
,得![]() .
.
又因为![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,所以
,所以![]() .
.
显然,当点![]() 与点
与点![]() 重合时,
重合时,![]() 取最大值2,此时
取最大值2,此时![]() ,
,
即三棱锥![]() 的体积的最大值为
的体积的最大值为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2.
(1)若曲线f(x)=xlnx在x=1处的切线与函数g(x)=﹣x2+ax﹣2也相切,求实数a的值;
(2)求函数f(x)在
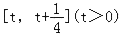 上的最小值;
上的最小值;(3)证明:对任意的x∈(0,+∞),都有
 成立
成立 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
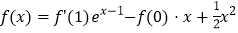 ,其中
,其中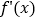 是函数
是函数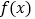 的导数.
的导数.(1)求
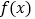 的单调区间;
的单调区间;(2)对于
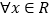 ,不等式
,不等式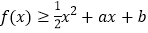 恒成立,求
恒成立,求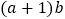 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设正项数列
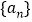 的前
的前 项和
项和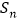 ,且满足
,且满足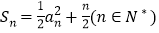 .
.(Ⅰ)计算
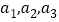 的值,猜想
的值,猜想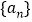 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;(Ⅱ)设
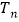 是数列
是数列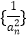 的前
的前 项和,证明:
项和,证明: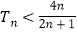 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
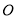 :
: 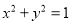 过椭圆
过椭圆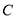 :
: 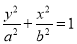 (
(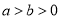 )的短轴端点,
)的短轴端点, 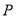 ,
, 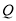 分别是圆
分别是圆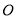 与椭圆
与椭圆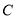 上任意两点,且线段
上任意两点,且线段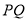 长度的最大值为3.
长度的最大值为3.(Ⅰ)求椭圆
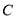 的方程;
的方程;(Ⅱ)过点
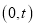 作圆
作圆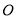 的一条切线交椭圆
的一条切线交椭圆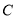 于
于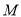 ,
, 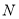 两点,求
两点,求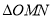 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照
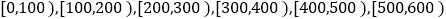 ,
,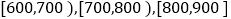 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.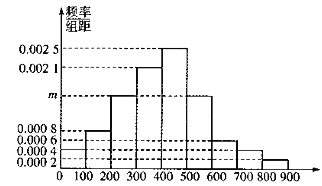
(1)求直方图中
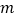 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用
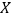 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量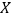 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
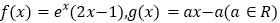
(1)若
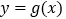 为曲线
为曲线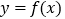 的一条切线,求a的值;
的一条切线,求a的值;(2)已知
 ,若存在唯一的整数
,若存在唯一的整数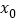 ,使得
,使得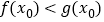 ,求a的取值范围.
,求a的取值范围.
相关试题

