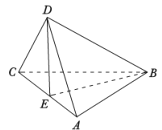
【题目】已知正方形![]() 的对角线
的对角线![]() 与
与![]() 相交于
相交于![]() 点,将
点,将![]() 沿对角线折起,使得平面
沿对角线折起,使得平面![]() 平面
平面![]() (如图),则下列命题中正确的是( )
(如图),则下列命题中正确的是( )
A. 直线![]() 直线
直线![]() ,且直线
,且直线![]() 直线
直线![]()
B. 直线![]() 平面
平面![]() ,且直线
,且直线![]() 平面
平面![]()
C. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
D. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
参考答案:
【答案】C
【解析】分析:由题意结合几何关系逐一考查所给命题的真假即可求得最终结果.
详解:若![]() ,则AB在平面ACD内的射影AC⊥CD,该结论明显不成立,则直线AB⊥直线CD不成立,故A错误;
,则AB在平面ACD内的射影AC⊥CD,该结论明显不成立,则直线AB⊥直线CD不成立,故A错误;
∵AB与CD不垂直,所以直线AB⊥平面BCD不成立,故B错误;
∵AC⊥DE,BE⊥AC,∴AC⊥平面BDE,∴平面ABC上平面BDE,
且平面ACD⊥平面BDE,故C正确;
很明显平面ABD⊥平面BCD不成立,故D错误.
本题选择C选项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
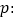 “直线
“直线 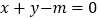 与圆
与圆 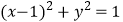 相交”;
相交”; 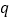 :“方程
:“方程 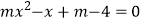 有一正根和一负根”.若
有一正根和一负根”.若 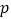 或
或 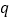 为真, 非p为真,求实数
为真, 非p为真,求实数 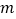 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,若函数
,若函数  在
在  处与直线
处与直线  相切.
相切.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数 在
在  上的最大值.
上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
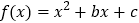 的图象过点(1,13),且函数
的图象过点(1,13),且函数
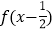 是偶函数.
是偶函数.(1)求
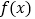 的解析式;
的解析式;(2)已知
 ,
,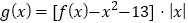 ,求函数
,求函数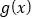 在[
在[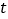 ,2]上的最大值和最小值;
,2]上的最大值和最小值;(3)函数
 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E、F.已知DE=1,将梯形ABCD沿AE、BF同侧折起,得空间几何体ADE﹣BCF,如图2.
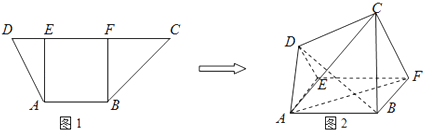
(Ⅰ)若AF⊥BD,证明:△BDE为直角三角形;
(Ⅱ)若DE∥CF,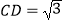 ,求平面ADC与平面ABFE所成角的余弦值.
,求平面ADC与平面ABFE所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
 中,过对角线
中,过对角线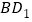 的一个平面交
的一个平面交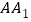 于点
于点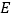 ,交
,交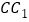 于
于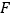 .
.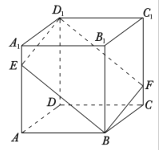
①四边形
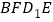 一定是平行四边形;
一定是平行四边形;②四边形
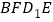 有可能是正方形;
有可能是正方形;③四边形
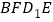 在底面
在底面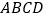 内的投影一定是正方形;
内的投影一定是正方形;④四边形
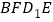 有可能垂直于平面
有可能垂直于平面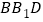 .
.以上结论正确的为_______________.(写出所有正确结论的编号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】求符合下列条件的直线方程:
(1)过点
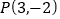 ,且与直线
,且与直线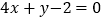 平行;
平行;(2)过点
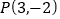 ,且与直线
,且与直线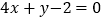 垂直;
垂直;(3)过点
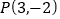 ,且在两坐标轴上的截距相等.
,且在两坐标轴上的截距相等.
相关试题

