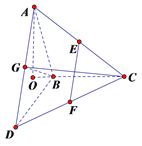
【题目】如图, ![]() 和
和![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
, ![]() 分别为AC、DC、AD的中点
分别为AC、DC、AD的中点

(1)求证: ![]() 平面BCG;
平面BCG;
(2)求三棱锥D-BCG的体积.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:()根据等腰三角形三线合一的性质,利用中点得垂直,再根据中位线的性质即可证出;(2)作出![]() ,交
,交![]() 的延长线于O,可证明
的延长线于O,可证明![]()
![]() 平面
平面![]() ,又G为AD的中点,故可求出三棱锥的高,底面积根据面积公式求出即可.
,又G为AD的中点,故可求出三棱锥的高,底面积根据面积公式求出即可.
试题解析:(1)由已知得, ![]() 是
是![]() 的中位线,故
的中位线,故![]() ,
,
则可转化为证明![]() 平面BCG.易证
平面BCG.易证![]() ,
,
则有![]() ,则在等腰三角形
,则在等腰三角形![]() 和等腰三角形
和等腰三角形![]() 中,
中, ![]() 是
是![]() 中点,
中点,
故![]() ,
, ![]() .从而
.从而![]() 平面BCG,进而
平面BCG,进而![]() 平面BCG;
平面BCG;
(2)在平面![]() 内,作
内,作![]() ,交
,交![]() 的延长线于O,由平面
的延长线于O,由平面![]()
![]() 平面
平面![]() ,
,
知![]()
![]() 平面
平面![]() .又∵ G为AD的中点,因此G到平面BCD的距离
.又∵ G为AD的中点,因此G到平面BCD的距离
![]() 是AO长度的一半;在
是AO长度的一半;在![]() 中,
中, ![]() ;
;
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)证明:函数
 在区间
在区间 上是减函数;
上是减函数;(2)当
 时,证明:函数
时,证明:函数 只有一个零点.
只有一个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
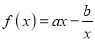 ,曲线
,曲线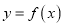 在点
在点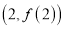 处的切线方程为
处的切线方程为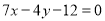 .
.(1)求
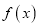 的解析式;
的解析式;(2)设
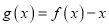 ,证明:函数
,证明:函数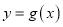 图象上任一点处的切线与两坐标轴所围成的三角形面积为定值,并求此定值.
图象上任一点处的切线与两坐标轴所围成的三角形面积为定值,并求此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设点
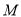 到坐标原点的距离和它到直线
到坐标原点的距离和它到直线 的距离之比是一个常数
的距离之比是一个常数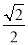 .
.(1)求点
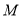 的轨迹;
的轨迹;(2)若
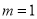 时得到的曲线是
时得到的曲线是 ,将曲线
,将曲线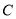 向左平移一个单位长度后得到曲线
向左平移一个单位长度后得到曲线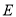 ,过点
,过点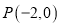 的直线
的直线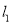 与曲线
与曲线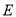 交于不同的两点
交于不同的两点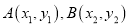 ,过
,过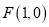 的直线
的直线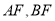 分别交曲线
分别交曲线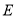 于点
于点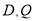 ,设
,设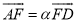 ,
, 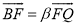 ,
, 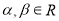 ,求
,求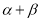 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初一年级500名学生参加某次数学测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:

(1)从总体的500名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的双曲线的标准方程:
(1)以椭圆
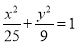 的长轴端点为焦点,且经过点P(5,
的长轴端点为焦点,且经过点P(5, 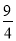 );
);(2)过点P1(3,-4
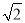 ),P2(
),P2( ,5).
,5). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是以线段BC为直径的圆O上一点,AD⊥BC于点D,过点B作圆O的切线,与CA的延长线相交于点E,点G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
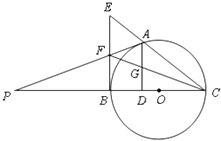
(1)求证:BF=EF;
(2)求证:PA是圆O的切线.
相关试题

