【题目】如图,点A是以线段BC为直径的圆O上一点,AD⊥BC于点D,过点B作圆O的切线,与CA的延长线相交于点E,点G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P. 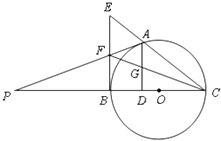
(1)求证:BF=EF;
(2)求证:PA是圆O的切线.
参考答案:
【答案】
(1)证明:∵BC是圆O的直径,BE是圆O的切线,∴EB⊥BC.
又∵AD⊥BC,∴AD∥BE.
可得△BFC∽△DGC,△FEC∽△GAC.
∴ ![]() ,得
,得 ![]() .
.
∵G是AD的中点,即DG=AG.
∴BF=EF
(2)证明:连接AO,AB.

∵BC是圆O的直径,∴∠BAC=90°.
由(1)得:在Rt△BAE中,F是斜边BE的中点,
∴AF=FB=EF,可得∠FBA=∠FAB.
又∵OA=OB,∴∠ABO=∠BAO.
∵BE是圆O的切线,
∴∠EBO=90°,得∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA⊥OA,由圆的切线判定定理,得PA是圆O的切线.
【解析】(1)利用平行线截三角形得相似三角形,得△BFC∽△DGC且△FEC∽△GAC,得到对应线段成比例,再结合已知条件可得BF=EF;(2)利用直角三角形斜边上的中线的性质和等边对等角,得到∠FAO=∠EBO,结合BE是圆的切线,得到PA⊥OA,从而得到PA是圆O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
,  分别为AC、DC、AD的中点
分别为AC、DC、AD的中点
(1)求证:
 平面BCG;
平面BCG;(2)求三棱锥D-BCG的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初一年级500名学生参加某次数学测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:

(1)从总体的500名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的双曲线的标准方程:
(1)以椭圆
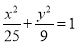 的长轴端点为焦点,且经过点P(5,
的长轴端点为焦点,且经过点P(5, 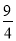 );
);(2)过点P1(3,-4
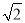 ),P2(
),P2( ,5).
,5). -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
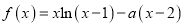 .
.(1)若
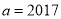 ,求曲线
,求曲线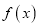 在
在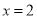 处的切线方程;
处的切线方程;(2)若当
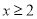 时,
时, 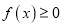 ,求
,求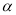 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ﹣
 )=
)= 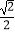 .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|﹣2≤x≤1}. (Ⅰ)求a的值;
(Ⅱ)若f(x)﹣2f( )≤k恒成立,求k的取值范围.
)≤k恒成立,求k的取值范围.
相关试题

