【题目】设点![]() 到坐标原点的距离和它到直线
到坐标原点的距离和它到直线![]() 的距离之比是一个常数
的距离之比是一个常数![]() .
.
(1)求点![]() 的轨迹;
的轨迹;
(2)若![]() 时得到的曲线是
时得到的曲线是![]() ,将曲线
,将曲线![]() 向左平移一个单位长度后得到曲线
向左平移一个单位长度后得到曲线![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,过
,过![]() 的直线
的直线![]() 分别交曲线
分别交曲线![]() 于点
于点![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析: (1)设![]() ,直接法求出点
,直接法求出点![]() 的轨迹方程,由轨迹方程判断出轨迹; (2)由已知条件求出曲线E的方程,利用向量坐标运算求出
的轨迹方程,由轨迹方程判断出轨迹; (2)由已知条件求出曲线E的方程,利用向量坐标运算求出![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,联立直线
,联立直线![]() 的方程和曲线E的方程,利用韦达定理求出
的方程和曲线E的方程,利用韦达定理求出![]() ,再求出
,再求出![]() 的范围.
的范围.
试题解析:(Ⅰ)过点![]() 作
作![]() ,
, ![]() 为垂足,
为垂足,
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
故点![]() 的轨迹方程为
的轨迹方程为![]() .
.
可化为![]() ,显然点
,显然点![]() 的轨迹为焦点在
的轨迹为焦点在![]() 轴上的椭圆.
轴上的椭圆.
(Ⅱ)![]() 时,得到的曲线
时,得到的曲线![]() 的方程是
的方程是![]() ,
,
故曲线![]() 的方程是
的方程是![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() .
.
当![]() 与
与![]() 轴不垂直时,直线
轴不垂直时,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,代入曲线
,代入曲线![]() 的方程并注意到
的方程并注意到![]() ,
,
整理可得![]() ,
,
则![]() ,即
,即![]() ,于是
,于是![]() .
.
当![]() 与
与![]() 轴垂直时,A点的横坐标为
轴垂直时,A点的横坐标为![]() ,
, ![]() ,显然
,显然![]() 也成立.
也成立.
同理可得![]() .
.
设直线![]() 的方程为
的方程为![]() ,联立
,联立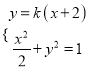 ,
,
消去y整理得![]() ,
,
由![]() 及
及![]() ,解得
,解得![]() .
.
又![]() ,
,
则![]() .
.
故求![]() 的取值范围是
的取值范围是![]() .
.
点睛:本题考查了轨迹方程的求法以及直线与椭圆相交时相关问题,属于中档题.在(1)中,求轨迹与求轨迹方程不一样,把轨迹方程求出来后,再判断是什么类型的曲线;在(2)中,注意向量坐标运算求出![]() 的表达式,再联立直线
的表达式,再联立直线![]() 的方程和椭圆方程求出
的方程和椭圆方程求出![]() ,进而求出
,进而求出![]() 的范围.
的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x(lnx﹣ax).
(1)a= 时,求f(x)在点(1,f(1))处的切线方程;
时,求f(x)在点(1,f(1))处的切线方程;
(2)若f(x)存在两个不同的极值x1 , x2 , 求a的取值范围;
(3)在(2)的条件下,求f(x)在(0,a]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)证明:函数
 在区间
在区间 上是减函数;
上是减函数;(2)当
 时,证明:函数
时,证明:函数 只有一个零点.
只有一个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
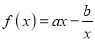 ,曲线
,曲线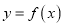 在点
在点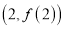 处的切线方程为
处的切线方程为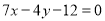 .
.(1)求
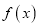 的解析式;
的解析式;(2)设
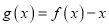 ,证明:函数
,证明:函数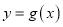 图象上任一点处的切线与两坐标轴所围成的三角形面积为定值,并求此定值.
图象上任一点处的切线与两坐标轴所围成的三角形面积为定值,并求此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
,  分别为AC、DC、AD的中点
分别为AC、DC、AD的中点
(1)求证:
 平面BCG;
平面BCG;(2)求三棱锥D-BCG的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初一年级500名学生参加某次数学测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:

(1)从总体的500名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的双曲线的标准方程:
(1)以椭圆
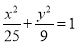 的长轴端点为焦点,且经过点P(5,
的长轴端点为焦点,且经过点P(5, 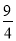 );
);(2)过点P1(3,-4
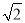 ),P2(
),P2( ,5).
,5).
相关试题

