【题目】若样本![]() 平均数是4,方差是2,则另一样本
平均数是4,方差是2,则另一样本![]() 的平均数和方差分别为( )
的平均数和方差分别为( )
A. 12,2 B. 14,6 C. 12,8 D. 14,18
参考答案:
【答案】D
【解析】
由已知条件推导出x1+x2+…+xn=n![]() ,从而得到3x1+2,3x2+2,…3xn+2的平均数是3
,从而得到3x1+2,3x2+2,…3xn+2的平均数是3![]() ,由
,由![]() [(x1﹣x)2+(x2﹣x)2+…+(xn﹣x)2]=s2,得到3x1+2,3x2+2,…3xn+2的方差是
[(x1﹣x)2+(x2﹣x)2+…+(xn﹣x)2]=s2,得到3x1+2,3x2+2,…3xn+2的方差是![]() [(x1
[(x1![]() )2+(x2
)2+(x2![]() )2+…+(xn
)2+…+(xn![]() )2],由此能求出结果.
)2],由此能求出结果.
∵x1,x2,…,xn 的平均数为![]() =4,
=4,
∴x1+x2+…+xn=n![]() ,
,
∴3x1+2,3x2+2,…3xn+2的平均数是:
(3x1+2+3x2+2+…+3xn+2)÷n
=[3(x1+x2+…+xn)+2n]÷n=(3n![]() 2n)÷n=3
2n)÷n=3![]() 2=14.
2=14.
∵x1,x2,…,xn 的方差为s2,
∴![]() [(x1﹣x)2+(x2﹣x)2+…+(xn﹣x)2]=s2,
[(x1﹣x)2+(x2﹣x)2+…+(xn﹣x)2]=s2,
∴3x1+2,3x2+2,…3xn+2的方差是:
![]() [(3x1+2﹣3
[(3x1+2﹣3![]() 2)2+(3x2+2﹣3
2)2+(3x2+2﹣3![]() 2)2+…+(3xn+2﹣3
2)2+…+(3xn+2﹣3![]() 2)2]
2)2]
![]() [(3x1﹣3
[(3x1﹣3![]() )2+(3x2﹣3
)2+(3x2﹣3![]() )2+…+(3xn﹣3
)2+…+(3xn﹣3![]() )2],
)2],
![]() [9(x1
[9(x1![]() )2+9(x2
)2+9(x2![]() )2+…+9(xn
)2+…+9(xn![]() )2],
)2],
![]() [(x1
[(x1![]() )2+(x2
)2+(x2![]() )2+…+(xn
)2+…+(xn![]() )2],
)2],
=9s2=18.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的最小值和最小正周期;
的最小值和最小正周期;(Ⅱ)已知
 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱锥
 中,
中, 为
为 中点,
中点, 为
为 中点,且
中点,且 为正三角形.
为正三角形.(I)求证:
 平面
平面 ;
;(II)求证:平面
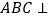 平面
平面 ;
;(III)若
 ,求三棱锥
,求三棱锥 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第
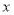 天的实验需投入实验费用为
天的实验需投入实验费用为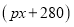 元
元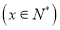 ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.(1)求
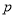 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;(2)现有某知名企业对该项实验进行赞助,实验
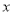 天共赞助
天共赞助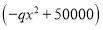 元
元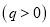 .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求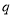 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角梯形
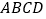 中,AB∥CD,
中,AB∥CD, ,且
,且 .现以
.现以 为一边向梯形外作正方形
为一边向梯形外作正方形 ,然后沿边
,然后沿边 将正方形
将正方形 翻折,使平面
翻折,使平面 与平面
与平面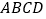 垂直,如图2.
垂直,如图2.

(Ⅰ)求证:BC⊥平面DBE;
(Ⅱ)求点D到平面BEC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的图象是由函数g(x)=cosx的图象经过如下变换得到:先将g(x)的图象向右平移
 个单位长度,再将其图象上所有点的横坐标变为原来的一半,纵坐标不变,则函数f(x)的图象的一条对称轴方程为( )
个单位长度,再将其图象上所有点的横坐标变为原来的一半,纵坐标不变,则函数f(x)的图象的一条对称轴方程为( )
A.x=
B.x=
C.x=
D.x=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员距篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:

(1)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(2)若从该运动员投篮命中时,他到篮筐中心的水平距离为2到5米的这三组中,用分层抽样的方法抽取7次成绩(单位:米,运动员投篮命中时,他到篮筐中心的水平距离越远越好),并从抽到的这7次成绩中随机抽取2次,并规定:成绩来自2到3米这一组时,记1分;成绩来自3到4米这一组时,记2分;成绩来4到5米的这一组记 4分,求该运动员2次总分不少于5分的概率.
相关试题

