【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)求出切点坐标及切线方程,切线恒过定点即与参数![]() 无关,令系数为
无关,令系数为![]() ,可得定点坐标;(2)
,可得定点坐标;(2)![]() ,要使
,要使![]() 成为极大值,因此
成为极大值,因此![]() ,又
,又![]() 不是最大值,而
不是最大值,而![]() 在
在![]() 单增,
单增,![]() 单减,
单减,![]() 单增,因此
单增,因此![]() ,可求得
,可求得![]() 的范围;(3)
的范围;(3)![]() 在
在![]() 单增,
单增,![]() 单减,
单减,![]() 单增,又
单增,又![]() ,所以要使
,所以要使![]() 在
在![]() 单调,只需
单调,只需![]() ,即
,即![]() ,故存在.
,故存在.
试题解析:解:(1)证明:∵![]() ,∴
,∴![]()
∵![]() ,∴曲线
,∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() ,令
,令![]() ,则
,则![]() ,
,
故曲线![]() 在点
在点![]() 处的切线过定点
处的切线过定点![]()
(2)解:![]() ,
,
令![]() 得
得![]() 或
或![]()
∵![]() 是
是![]() 在区间
在区间![]() 上的极大值,∴
上的极大值,∴![]() ,∴
,∴![]()
令![]() ,得
,得![]() 或
或![]() 递增;令
递增;令![]() ,得
,得![]() 递减,
递减,
∵![]() 不是
不是![]() 在区间
在区间![]() 上的最大值,
上的最大值,
∴![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
∴![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]()
(3)证明:![]() ,
,
∵![]() ,∴
,∴![]()
令![]() ,得
,得![]() 或
或![]() 递增;令
递增;令![]() ,得
,得![]() 递减,
递减,
∵![]() ,∴
,∴![]()
若![]() 在
在![]() 上为单调函数,则
上为单调函数,则![]() ,即
,即![]()
故对任意给定的正数![]() ,总存在
,总存在![]() (其中
(其中![]() ),使得
),使得![]() 在
在![]() 上为单调函数
上为单调函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了对某课题进行研究,用分层抽样方法从三所高校
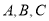 的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
(1)求
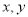 ;
;(2)若从高校
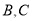 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校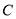 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
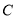 :
:  的短轴长为2,且函数
的短轴长为2,且函数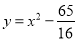 的图象与椭圆
的图象与椭圆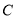 仅有两个公共点,过原点的直线
仅有两个公共点,过原点的直线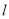 与椭圆
与椭圆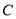 交于
交于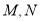 两点.
两点.(1)求椭圆
 的标准方程;
的标准方程;(2)点
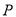 为线段
为线段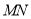 的中垂线与椭圆
的中垂线与椭圆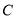 的一个公共点,求
的一个公共点,求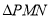 面积的最小值,并求此时直线
面积的最小值,并求此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五棱锥
 中,平面
中,平面 平面
平面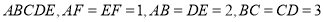 ,且
,且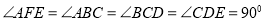 .
.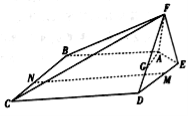
(1)已知点
 在线段
在线段 上,确定
上,确定 的位置,使得
的位置,使得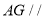 平面
平面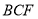 ;
;(2)点
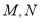 分别在线段
分别在线段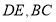 上,若沿直线
上,若沿直线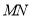 将四边形
将四边形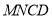 向上翻折,
向上翻折,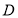 与
与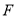 恰好重合,求直线
恰好重合,求直线 与平面
与平面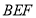 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
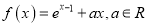 .
.(1)讨论函数
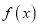 的单调区间;
的单调区间;(2)若
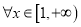 ,
, 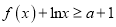 恒成立,求
恒成立,求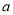 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)
 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?(2)估计这次环保知识竞赛的及格率(60分及以上为及格).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
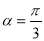 .
.(1)写出所有与
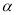 终边相同的角;
终边相同的角;(2)写出在
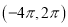 内与
内与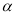 终边相同的角;
终边相同的角;(3)若角
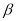 与
与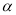 终边相同,则
终边相同,则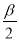 是第几象限的角?
是第几象限的角?
相关试题

