【题目】已知设函数 ![]() .
.
(1)求 ![]() 的定义域;
的定义域;
(2)判断 ![]() 的奇偶性并予以证明;
的奇偶性并予以证明;
(3)求使 ![]() 的
的 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)奇函数;(3)见解析.
;(2)奇函数;(3)见解析.
【解析】试题分析:(1)根据对数函数的图象与性质,列出函数有意义所满足的条件,即可求解函数的定义域;
(2)根据函数奇偶性的定义,即可判定函数![]() 的奇偶性;
的奇偶性;
(3)由(2)化简得![]() ,再根据对数函数的性质,分
,再根据对数函数的性质,分![]() 和
和![]() 两种情况讨论,即可求解
两种情况讨论,即可求解![]() 的取值范围.
的取值范围.
试题解析:
(1) ![]() 所以
所以 ![]() 的定义域为
的定义域为 ![]() .
.
(2) 定义域为 ![]() ,关于原点对称
,关于原点对称
又因为 ![]()
所以 ![]() 为奇函数.
为奇函数.
(3) ![]()
当 ![]() 时,原不等式等价为:
时,原不等式等价为: ![]()
当 ![]() 时,原不等式等价为:
时,原不等式等价为: ![]()
又因为 ![]() 的定义域为
的定义域为 ![]()
所以使 ![]() 的
的 ![]() 的取值范围,当
的取值范围,当 ![]() 时为
时为 ![]() ;当
;当 ![]() 时为
时为 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,函数
,函数 
(1)若
 在
在  上单调递增,求
上单调递增,求  的取值范围;
的取值范围;(2)记
 为
为  在
在 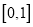 上的最大值,求
上的最大值,求 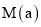 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时,学生的兴趣激增;接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.设
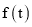 表示学生注意力指标,该小组发现
表示学生注意力指标,该小组发现 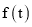 随时间
随时间 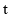 (分钟)的变化规律(
(分钟)的变化规律(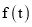 越大,表明学生的注意力越集中)如下:
越大,表明学生的注意力越集中)如下: 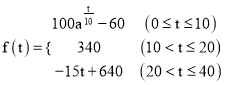 (
(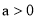 ,且
,且 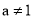 )
)若上课后第
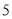 分钟时的注意力指标为
分钟时的注意力指标为 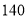 ,回答下列问题:
,回答下列问题:(1)求
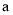 的值;
的值;(2)上课后第
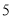 分钟时和下课前
分钟时和下课前 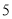 分钟时比较,哪个时间注意力更集中?并请说明理由.
分钟时比较,哪个时间注意力更集中?并请说明理由.(3)在一节课中,学生的注意力指标至少达到
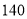 的时间能保持多长?
的时间能保持多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
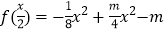 ,
,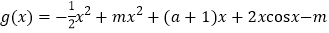 .
.(1)若曲线
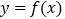 仅在两个不同的点
仅在两个不同的点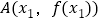 ,
,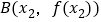 处的切线都经过点
处的切线都经过点 ,求证:
,求证: ,或
,或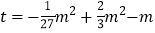 ;
;(2)当
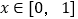 时,若
时,若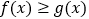 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
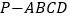 中,侧面
中,侧面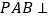 底面
底面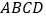 ,
,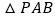 为正三角形,
为正三角形,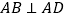 ,
,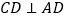 ,点
,点 ,
, 分别为线段
分别为线段 、
、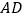 的中点,
的中点,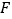 、
、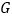 分别为线段
分别为线段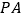 、
、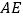 上一点,且
上一点,且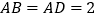 ,
,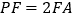 .
.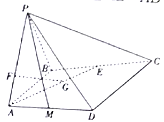
(1)确定点
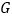 的位置,使得
的位置,使得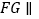 平面
平面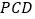 ;
;(2)试问:直线
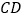 上是否存在一点
上是否存在一点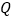 ,使得平面
,使得平面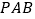 与平面
与平面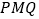 所成锐二面角的大小为
所成锐二面角的大小为 ,若存在,求
,若存在,求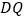 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
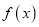 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意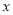 ,恒有
,恒有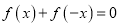 ;②对于定义域上的任意
;②对于定义域上的任意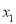 ,
, 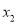 ,当
,当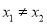 时,恒有
时,恒有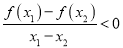 ,则称函数
,则称函数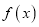 为“理想函数”.在下列三个函数中:(1)
为“理想函数”.在下列三个函数中:(1)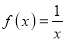 ;(2)
;(2)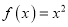 ;(3)
;(3)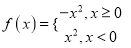 .“理想函数”有__________.(只填序号)
.“理想函数”有__________.(只填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的程序框图,当输入的x的值为0和4时,输出的值相等,根据该图和下列各小题的条件解答下面的几个问题.

(1)该程序框图解决的是一个什么问题?
(2)当输入的x的值为3时,求输出的f(x)的值;
(3)要想使输出的值最大,求输入的x的值.
相关试题

