【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率
)的离心率![]() ,直线
,直线![]() 被以椭圆
被以椭圆![]() 的短轴为直径的圆截得的弦长为
的短轴为直径的圆截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两个不同的点,且
两个不同的点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:
(1)由直线与圆的位置关系可得![]() .由椭圆的离心率可得
.由椭圆的离心率可得![]() ,则椭圆
,则椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() ,当直线
,当直线![]() 的斜率不为
的斜率不为![]() 时,设直线
时,设直线![]() 在y轴上的截距式方程为
在y轴上的截距式方程为![]() ,
, ![]() ,
, ![]() ,联立方程可得
,联立方程可得![]() ,满足题意时
,满足题意时![]() ,结合韦达定理可知
,结合韦达定理可知![]() ,据此可知
,据此可知![]() .综上可得
.综上可得![]() .
.
试题解析:
(1)因为原点到直线![]() 的距离为
的距离为![]() ,
,
所以 (
(![]() ),解得
),解得![]() .
.
又![]() ,得
,得![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() ,
,
当直线![]() 的斜率不为
的斜率不为![]() 时,设直线
时,设直线![]() :
: ![]() ,
, ![]() ,
, ![]() ,
,
联立方程组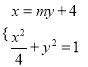 ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,
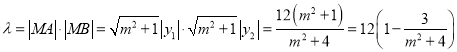 ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.
综上可得: ![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 也为抛物线
也为抛物线 的焦点.(1)若
的焦点.(1)若 为椭圆
为椭圆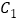 上两点,且线段
上两点,且线段 的中点为
的中点为 ,求直线
,求直线 的斜率;
的斜率;(2)若过椭圆
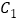 的右焦点
的右焦点 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于 和
和 ,设线段
,设线段 的长分别为
的长分别为 ,证明
,证明 是定值.
是定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】
某初级中学共有学生2000名,各年级男、女生人数如下表:
初一年级
初二年级
初三年级
女生
373
x
y
男生
377
370
z
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
求x的值;
现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
已知y
 245,z
245,z 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了一次新高考质量测评,在成绩统计分析中,某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
5
6
8
6
2
3
3
5
6
8
9
7
1
2
2
3
4
5
6
7
8
9
8
9
5
8

(1)求该班数学成绩在
 的频率及全班人数;
的频率及全班人数;(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定90分及其以上为优秀,现从该班分数在80分及其以上的试卷中任取2份分析学生得分情况,求在抽取的2份试卷中至少有1份优秀的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节对同一类的
 ,
, ,
, ,
, 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是
 或
或 作品获得一等奖”;
作品获得一等奖”;乙说:“
 作品获得一等奖”;
作品获得一等奖”;丙说:“
 ,
, 两项作品未获得一等奖”;
两项作品未获得一等奖”;丁说:“是
 作品获得一等奖”.
作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为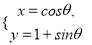 (
( 为参数),曲线
为参数),曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数).(1)将
 ,
,  的方程化为普通方程,并说明它们分别表示什么曲线?
的方程化为普通方程,并说明它们分别表示什么曲线?(2)以坐标原点为极点,以
 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线 的极坐标方程为
的极坐标方程为 .若
.若 上的点
上的点 对应的参数为
对应的参数为 ,点
,点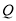 在
在 上,点
上,点 为
为 的中点,求点
的中点,求点 到直线
到直线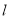 距离的最小值.
距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
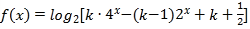 .
.(1)当
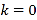 时,求函数的值域;
时,求函数的值域;(2)若函数
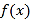 的最大值是
的最大值是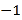 ,求
,求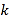 的值;
的值;(3)已知
 ,若存在两个不同的正数
,若存在两个不同的正数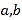 ,当函数
,当函数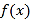 的定义域为
的定义域为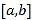 时,
时,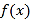 的值域为
的值域为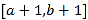 ,求实数
,求实数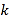 的取值范围.
的取值范围.
相关试题

