【题目】如图:在正方体ABCD﹣A1B1C1D1中,E为棱DD1的中点
(1)求证:BD1∥平面AEC
(2)求证:AC⊥BD1 . 
参考答案:
【答案】证明:(1)连接BD交AC于F,连EF.
因为F为正方形ABCD对角线的交点,
所长F为AC、BD的中点.
在DD1B中,E、F分别为DD1、DB的中点,
所以EF∥D1B.
又EF平面EAC,所以BD1∥平面EAC.
(2)由正方形的性质可得AC⊥BD
又由正方体的几何特征可得:D1D⊥平面ABCD
又∵AC平面ABCD
∴AC⊥D1D
又∵D1D∩BD=D
∴AC⊥平面D1DB
∵BD1平面D1DB
∴AC⊥BD1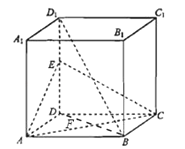
【解析】(1)欲证BD1∥平面EAC,只需在平面EAC内找一条直线BD1与平行,根据中位线定理可知EF∥D1B,满足线面平行的判定定理所需条件,即可得到结论;
(2)根据正方形的性质及正方体的几何特征,结合线面垂直的性质,可得AC⊥BD,AC⊥D1D,由线面垂直的判定定理可得AC⊥平面D1DB,再由线面垂直的性质即可得到AC⊥BD1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差大于零的等差数列
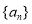 的前
的前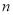 项和为
项和为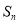 ,且
,且 ,
,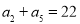 .
.(1)求数列
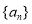 的通项公式;
的通项公式;(2)若数列
 是等差数列,且
是等差数列,且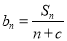 ,求非零常数
,求非零常数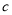 的值.
的值.(3)设
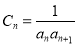 ,
,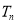 为数列
为数列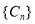 的前
的前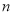 项和,是否存在正整数
项和,是否存在正整数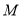 ,使得
,使得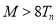 对任意的
对任意的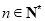 均成立?若存在,求出
均成立?若存在,求出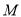 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=
 , AD=1,DC⊥BC,则这块菜地的面积为
, AD=1,DC⊥BC,则这块菜地的面积为 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (x﹣2)的定义域为集合A,函数
(x﹣2)的定义域为集合A,函数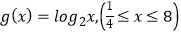 的值域为集合B.
的值域为集合B.
(1)求A∪B;
(2)若集合C={x|a≤x≤3a﹣1},且B∩C=C,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,空间几何体
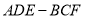 中,四边形
中,四边形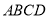 是梯形,四边形
是梯形,四边形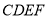 是矩形,且平面
是矩形,且平面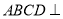 平面
平面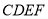 ,
,  ,
, 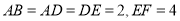 ,
, 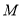 是线段
是线段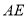 上的动点.
上的动点.(1)求证:
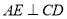 ;
;(2)试确定点
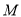 的位置,使
的位置,使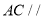 平面
平面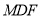 ,并说明理由;
,并说明理由;(3)在(2)的条件下,求空间几何体
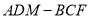 的体积.
的体积.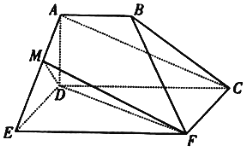
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过20万元时,按销售利润的20%进行奖励;当销售利润超过20万元时,若超出部分为A万元,则超出部分按2log5(A+2)进行奖励,没超出部分仍按销售利润的20%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员奖励方案的函数表达式;
(2)如果业务员老张获得8万元的奖励,那么他的销售利润是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:
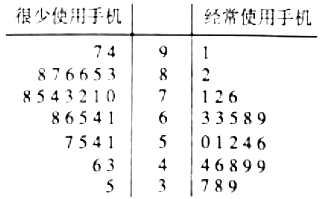
(1)根据茎叶图中的数据完成下面的
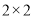 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?及格(
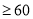 )
)不及格
合计
很少使用手机
经常使用手机
合计
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为
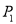 ,
, 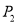 ,
, 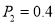 ,若
,若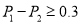 ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记 为两人中解决此题的人数,若
为两人中解决此题的人数,若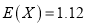 ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?参考公式及数据:
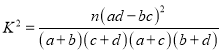 ,其中
,其中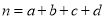 .
.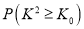
0.10
0.05
0.025
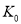
2.706
3.841
5.024
相关试题

