【题目】已知椭圆E的右焦点与抛物线![]() 的焦点重合,点M
的焦点重合,点M![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)设![]() ,直线
,直线![]() 与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求
与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(1)求出抛物线的焦点,可得椭圆的焦点,即![]() ,再由椭圆的定义,结合两点的距离公式,可得
,再由椭圆的定义,结合两点的距离公式,可得![]() ,由
,由![]() 的关系,可得
的关系,可得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)由题意可得![]() ,设
,设![]() ,运用两点的斜率公式和点在直线上,将直线
,运用两点的斜率公式和点在直线上,将直线![]() 代入椭圆方程,运用韦达定理,代入可得
代入椭圆方程,运用韦达定理,代入可得![]() 的方程,化简整理,解方程可得
的方程,化简整理,解方程可得![]() 的值.
的值.
试题解析:
(Ⅰ) 因为抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,所以
,所以![]() ,
,
所以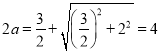 ,
,
即![]() .因为
.因为![]() ,
,
所以椭圆E的方程为![]() .
.
(Ⅱ)设![]() ,
,
联立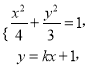 得
得![]() ,
, ![]()
所以![]() , ①
, ①
因为直线PA, PB关于x轴对称,
所以![]() ,
,
即![]() ,
,
通分得![]() ,
,
所以![]()
整理,得![]() . ②
. ②
将①代入②,得 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有些家用电器(如冰箱等)使用了氟化物,氟化物的释放破坏了大气上层的臭氧层,使臭氧含量呈指数型函数变化,在氟化物排放量维持某种水平时,具有关系式Q=Q0e-0.0025t,其中Q0是臭氧的初始量.
(1)随着时间t的增加,臭氧的含量是增加的还是减少的?
(2)试估计多少年以后将会有一半的臭氧消失?(参考数据:ln 0.5=-0.69)
-
科目: 来源: 题型:
查看答案和解析>>【题目】.已知函数f(x)=x2-2x-3,若x∈[t,t+2]时,求函数f(x)的最值.
-
科目: 来源: 题型:
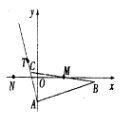
查看答案和解析>>【题目】如图,已知
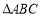 的边
的边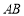 所在直线的方程为
所在直线的方程为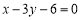 ,
,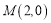 满足
满足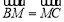 ,点
,点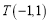 在
在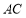 边所在直线上且满足
边所在直线上且满足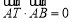 .
.
(1)求
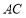 边所在直线的方程;
边所在直线的方程;(2)求
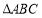 外接圆的方程;
外接圆的方程;(3)若动圆
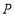 过点
过点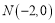 ,且与
,且与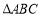 的外接圆外切,求动圆
的外接圆外切,求动圆 的圆心的轨迹方程.
的圆心的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
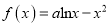 .
.(1)当
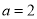 时,求函数
时,求函数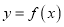 在
在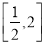 上的最大值;
上的最大值;(2)令
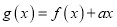 ,若
,若 在区间
在区间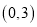 上为单调递增函数,求
上为单调递增函数,求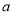 的取值范围;
的取值范围;(3)当
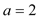 时,函数
时,函数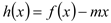 的图象与
的图象与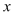 轴交于两点
轴交于两点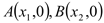 ,且
,且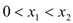 ,又
,又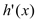 是
是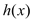 的导函数.若正常数
的导函数.若正常数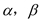 满足条件
满足条件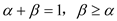 .试比较
.试比较 与0的关系,并给出理由.
与0的关系,并给出理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
相关试题

