【题目】已知集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
)x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
(1)求集合A∩B,(UB)∪A;
(2)若A∪C=A,求实数a的取值范围.
参考答案:
【答案】
(1)解:由题意:U=R,
集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9}={x|﹣1≤x≤2};
)x﹣1≤9}={x|﹣1≤x≤2};
集合B={x|log2x<3}={x|0<x<8};
则:UB={x|0≥x或8≤x};
集合C={x|x2﹣(2a+1)x+a2+a≤0}={x|a≤x≤a+1}
∴集合A∩B={x|0<x≤2};
(UB)∪A={x|x≤2或8≤x}
(2)解:由题意:A∪C=A,
∴CA,
则满足: ![]() ,
,
解得:﹣1≤a≤1
所以实数a的取值范围是[﹣1,1]
【解析】(1)确定集合A,集合B的组成范围,根据集合的基本运算即可求A∩B,(UB)∪A;(2)根据A∪C=A,建立条件关系即可求实数a的取值范围.
【考点精析】本题主要考查了交、并、补集的混合运算的相关知识点,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29.
(1)求数列{an}的通项公式;
(2)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在D上的函数f(x)若同时满足:①存在M>0,使得对任意的x1 , x2∈D,都有|f(x1)﹣f(x2)|<M;②f(x)的图象存在对称中心.则称f(x)为“P﹣函数”.
已知函数f1(x)=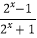 和f2(x)=lg(
和f2(x)=lg( 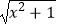 ﹣x),则以下结论一定正确的是( )
﹣x),则以下结论一定正确的是( )
A.f1(x)和 f2(x)都是P﹣函数
B.f1(x)是P﹣函数,f2(x)不是P﹣函数
C.f1(x)不是P﹣函数,f2(x)是P﹣函数
D.f1(x)和 f2(x)都不是P﹣函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=|ax﹣1﹣1|在区间(a,3a﹣1)上单调递减,则实数a的取值范围是 .
-
科目: 来源: 题型:
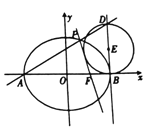
查看答案和解析>>【题目】如图,设椭圆
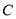 :
: 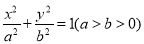 的离心率为
的离心率为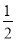 ,
, 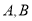 分别为椭圆
分别为椭圆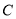 的左、右顶点,
的左、右顶点,  为右焦点,直线
为右焦点,直线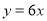 与
与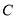 的交点到
的交点到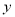 轴的距离为
轴的距离为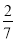 ,过点
,过点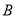 作
作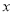 轴的垂线
轴的垂线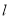 ,
, 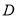 为
为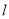 上异于点
上异于点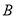 的一点,以
的一点,以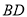 为直径作圆
为直径作圆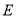 .
.
(1)求
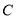 的方程;
的方程;(2)若直线
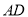 与
与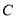 的另一个交点为
的另一个交点为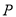 ,证明:直线
,证明:直线 与圆
与圆 相切.
相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】若椭圆C1:
 的离心率等于
的离心率等于  ,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
(1)求抛物线C2的方程;
(2)求过点M(﹣1,0)的直线l与抛物线C2交E、F两点,又过E、F作抛物线C2的切线l1、l2 , 当l1⊥l2时,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣1﹣x.
(1)若存在x∈[﹣1,ln ],满足a﹣ex+1+x<0成立,求实数a的取值范围.
],满足a﹣ex+1+x<0成立,求实数a的取值范围.
(2)当x≥0时,f(x)≥(t﹣1)x恒成立,求实数t的取值范围.
相关试题

