【题目】某地政府调查了工薪阶层![]() 人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是
人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是![]() .(单位:百元)
.(单位:百元)

(1)为了了解工薪阶层对工资收人的满意程度,要用分层抽样的方法从调查的![]() 人中抽取
人中抽取![]() 人做电话询问,求月工资收人在
人做电话询问,求月工资收人在![]() 内应抽取的人数;
内应抽取的人数;
(2)根据频率分布直方图估计这![]() 人的平均月工资为多少元.
人的平均月工资为多少元.
参考答案:
【答案】(1)15;(2)2400.
【解析】试题分析:
(1)由分层抽样的定义可得月工资收人在![]() 内应抽取的人数为15人;
内应抽取的人数为15人;
(2)利用频率分布直方图可求得根据频率分布直方图估计这![]() 人的平均月工资为2400元.
人的平均月工资为2400元.
试题解析:
(1)由频率发布直方图可得![]() 月工资收入段所占频率为
月工资收入段所占频率为![]() ,所以抽取
,所以抽取![]() 人中
人中![]() 收入段的人数为
收入段的人数为![]() (人).
(人).
(2)这![]() 人平均工资的估计值为
人平均工资的估计值为![]()
![]() (百元)
(百元)![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
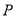 是椭圆
是椭圆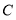 上任一点,点
上任一点,点 到直线
到直线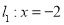 的距离为
的距离为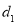 ,到点
,到点 的距离为
的距离为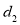 ,且
,且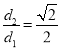 .直线
.直线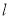 与椭圆
与椭圆 交于不同两点
交于不同两点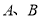 (
( 都在
都在 轴上方),且
轴上方),且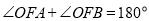 .
.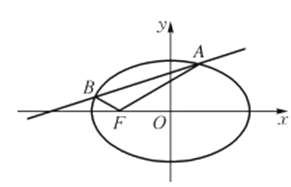
(1)求椭圆
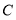 的方程;
的方程;(2)当
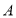 为椭圆与
为椭圆与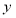 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线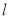 方程;
方程;(3)对于动直线
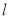 ,是否存在一个定点,无论
,是否存在一个定点,无论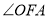 如何变化,直线
如何变化,直线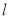 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
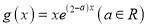 ,
, 为自然对数的底数.
为自然对数的底数.(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)若函数
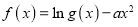 的图象与直线
的图象与直线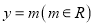 交于
交于 两点,线段
两点,线段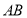 中点的横坐标为
中点的横坐标为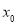 ,证明:
,证明: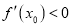 (
(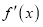 为函数
为函数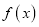 的导函数)
的导函数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
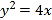 ,
,  是焦点,直线
是焦点,直线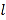 是经过点
是经过点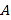 的任意直线.
的任意直线.(Ⅰ)若直线
 与抛物线交于
与抛物线交于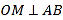 、
、 两点,且
两点,且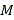 (
(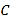 是坐标原点,
是坐标原点,  是垂足),求动点
是垂足),求动点 的轨迹方程;
的轨迹方程;(Ⅱ)若
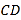 、
、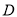 两点在抛物线
两点在抛物线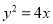 上,且满足
上,且满足 ,求证:直线
,求证:直线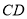 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
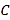 :
:  (
( )的两个焦点为
)的两个焦点为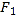 ,
, 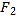 ,离心率为
,离心率为 ,点
,点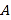 ,
, 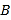 在椭圆上,
在椭圆上, 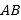 在线段
在线段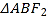 上,且
上,且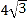 的周长等于
的周长等于 .
.(Ⅰ)求椭圆
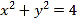 的标准方程;
的标准方程;(Ⅱ)过圆
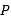 :
:  上任意一点
上任意一点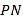 作椭圆
作椭圆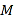 的两条切线
的两条切线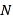 和
和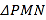 与圆
与圆 交于点
交于点 ,
, 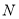 ,求
,求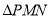 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
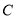 :
: 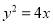 的焦点为
的焦点为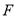 ,过点
,过点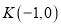 的直线
的直线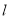 与
与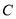 相交于
相交于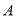 、
、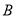 两点,点
两点,点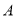 关于
关于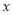 轴的对称点为
轴的对称点为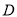 .
.(Ⅰ)判断点
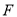 是否在直线
是否在直线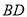 上,并给出证明;
上,并给出证明;(Ⅱ)设
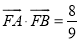 ,求
,求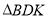 的内切圆
的内切圆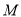 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入
 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )8
3
4
1
5
9
6
7
2
A. 9 B. 8 C. 6 D. 4
相关试题

